Question

Using integration, find the area of the region bounded by the line $y=1+\left| x+1 \right|,x=-2,x=3\ and\ y=0$.

Answer 1

Hint: We will first start by drawing the graph of curves $y=1+\left| x+1 \right|,x=-2,x=3\ and\ y=0$. Then we will use the fact that the algebraic area under a curve $f\left( x \right)$ can be found by integration as $\int{f\left( x \right)dx}$.

Complete step-by-step answer:
Now, before starting the solution we first to understand that the physical significance of $\int\limits_{a}^{b}{f\left( x \right)dx}$ is,

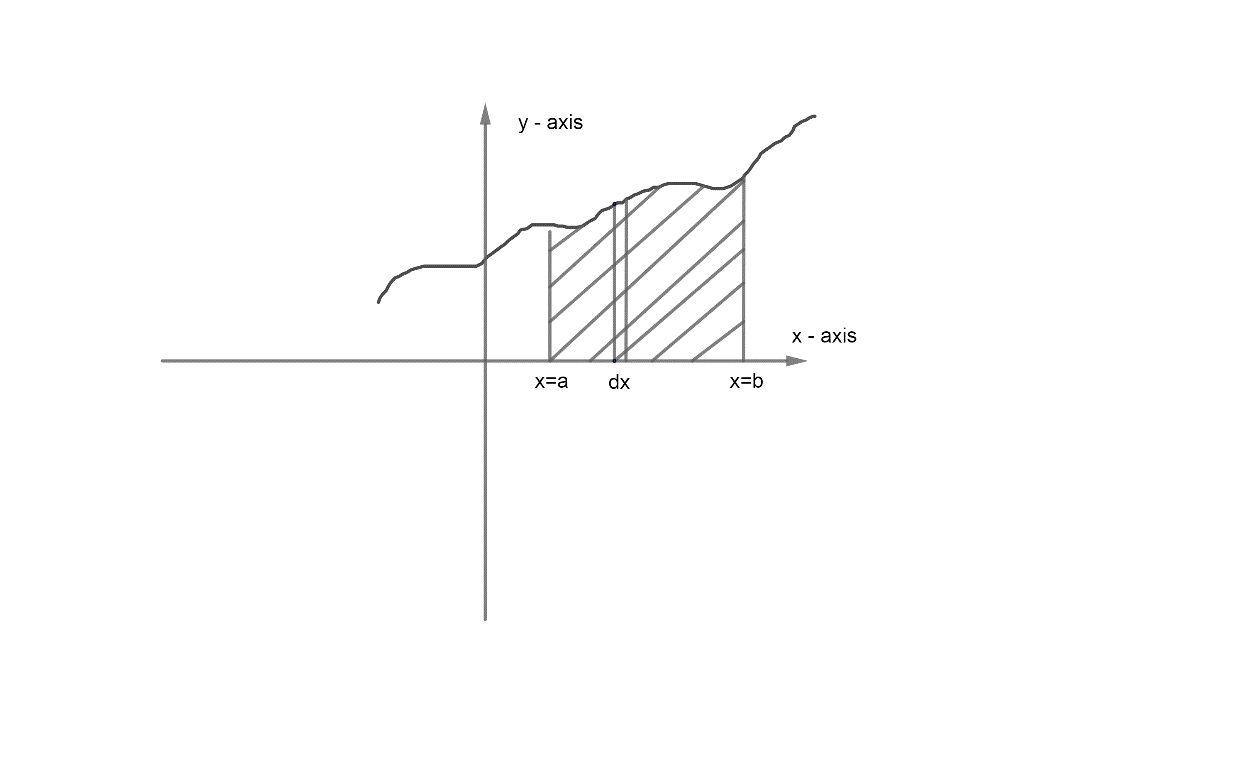
Now, we can see from the graph that $\int\limits_{a}^{b}{f\left( x \right)dx}$ is nothing but the area bounded by the line $y=f\left( x \right),x=a,x=b\ and\ x-axis$.
Now, we know that the graph of $y=1+\left| x+1 \right|$ is shifted 1 units upward and 1 units leftwards from the origin of the graph of $y=\left( x \right)$. So, we have the graph by using the concept of shifted origin as,

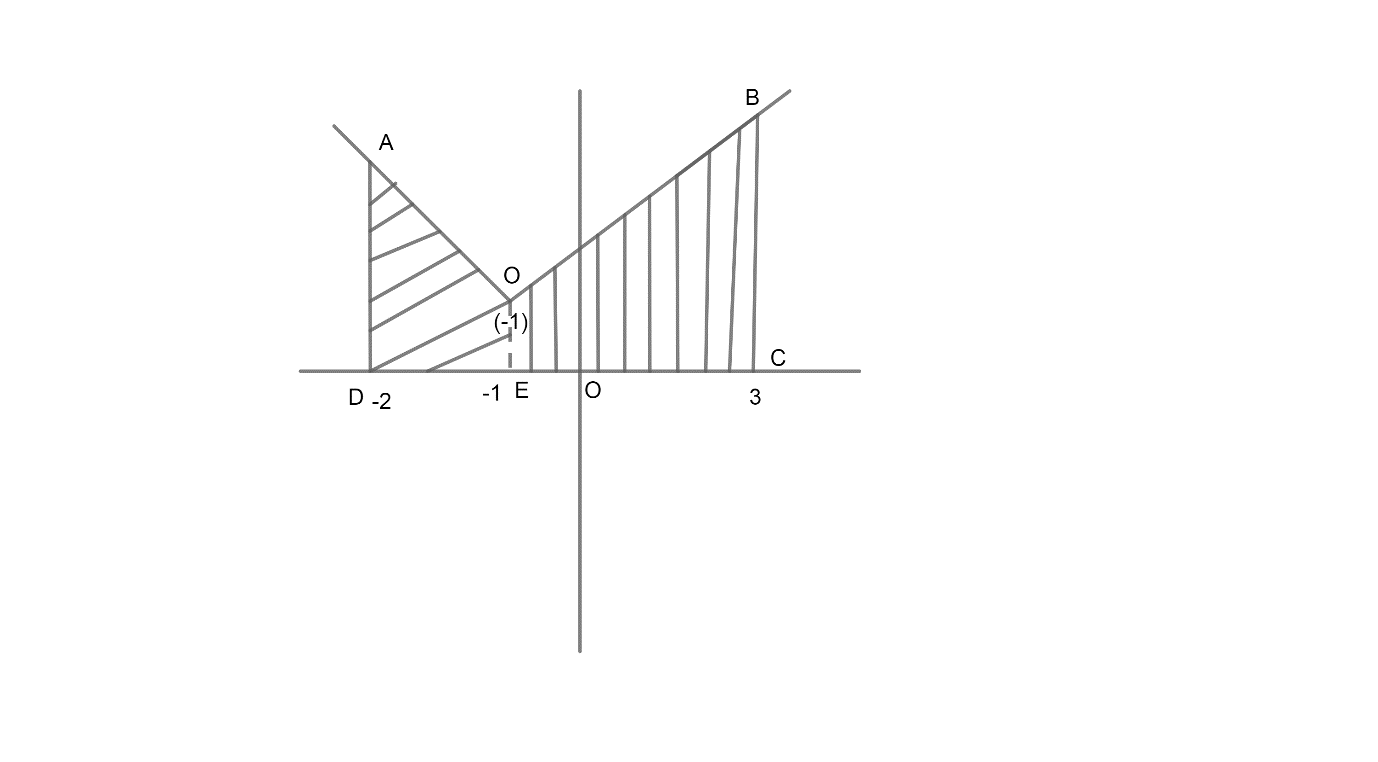
Now, we will first find the area of region ADEO. So, we have the equation of line AO as,
$\begin{aligned} & y=1-x-1 \\\ & \Rightarrow y=-x \\\ \end{aligned}$
So, we have the area of region,
$ADEO=\int\limits_{-2}^{-1}{\left( -x \right)dx}$
We have put the limits as x = -1 to x = -2 from the graph. Also, we know that $\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}$. So, we have,
$\begin{aligned} & \Rightarrow \left. \dfrac{-{{x}^{2}}}{2} \right|_{-2}^{-1} \\\ & \Rightarrow \left( \dfrac{{{\left( -1 \right)}^{2}}}{2}-\dfrac{{{\left( -2 \right)}^{2}}}{2} \right) \\\ & \Rightarrow -\left( \dfrac{1}{2}-2 \right) \\\ & \Rightarrow -\left( -\dfrac{3}{2} \right) \\\ & \Rightarrow \dfrac{3}{2}sq\ units \\\ \end{aligned}$
Now, similarly we will find the area of region OECB as,
$\int\limits_{-1}^{3}{\left( x+2 \right)dx}$
We have put the limits as x = -1 to x = 3 by referring the graph and again using the fact that $\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}$. We have,
$\begin{aligned} & \Rightarrow \left( \dfrac{{{x}^{2}}}{2}+2x \right)_{-1}^{3} \\\ & \Rightarrow \left( \dfrac{{{3}^{2}}}{2}-\dfrac{{{\left( -1 \right)}^{2}}}{2}+2\left( 3-\left( -1 \right) \right) \right) \\\ & \Rightarrow \left( \dfrac{9}{2}-\dfrac{1}{2}+2\left( 3+1 \right) \right) \\\ & \Rightarrow \left( \dfrac{9-1}{2}+2\times 4 \right) \\\ & \Rightarrow \left( \dfrac{8}{2}+2\times 4 \right) \\\ & \Rightarrow 4+8 \\\ & \Rightarrow 12sq\ units \\\ \end{aligned}$
So, the total area bounded by the region is,
ar of region ADEO + ar of region OECD
$\begin{aligned} & \Rightarrow \dfrac{3}{2}+12 \\\ & \Rightarrow \dfrac{3+24}{2} \\\ & \Rightarrow \dfrac{27}{2}sq\ units \\\ \end{aligned}$
Therefore, the total area bounded by the given curves is $\dfrac{27}{2}sq\ units$.

Note: While solving the question it is important to note how we have drawn the graph of $\left( y-1 \right)=\left| x-\left( -1 \right) \right|$ from the graph of $y=\left| x \right|$ by using the concept of shifted origin.