Question

Using integration, find the area of the $\Delta ABC$, the equations of whose sides AB, BC and AC are given by $y=4x+5,x+y=5\ and\ 4y=x+5$ respectively.

Answer 1

We will start by drawing a rough diagram of the triangle by plotting the given lines and finding their point of intersection. Then we will divide the area into parts as per the graph to find the area of that region with the help of the integration as we know that the area given by integration is algebraic rather than geometric meaning that if the curve is below x-axis then the area will be negative so we have to calculate the area of such parts separately by using integration and add them to find the overall area.

Complete step-by-step answer:
Now, before starting the solution we first to understand that the physical significance of $\int\limits_{a}^{b}{f\left( x \right)dx}$ is,

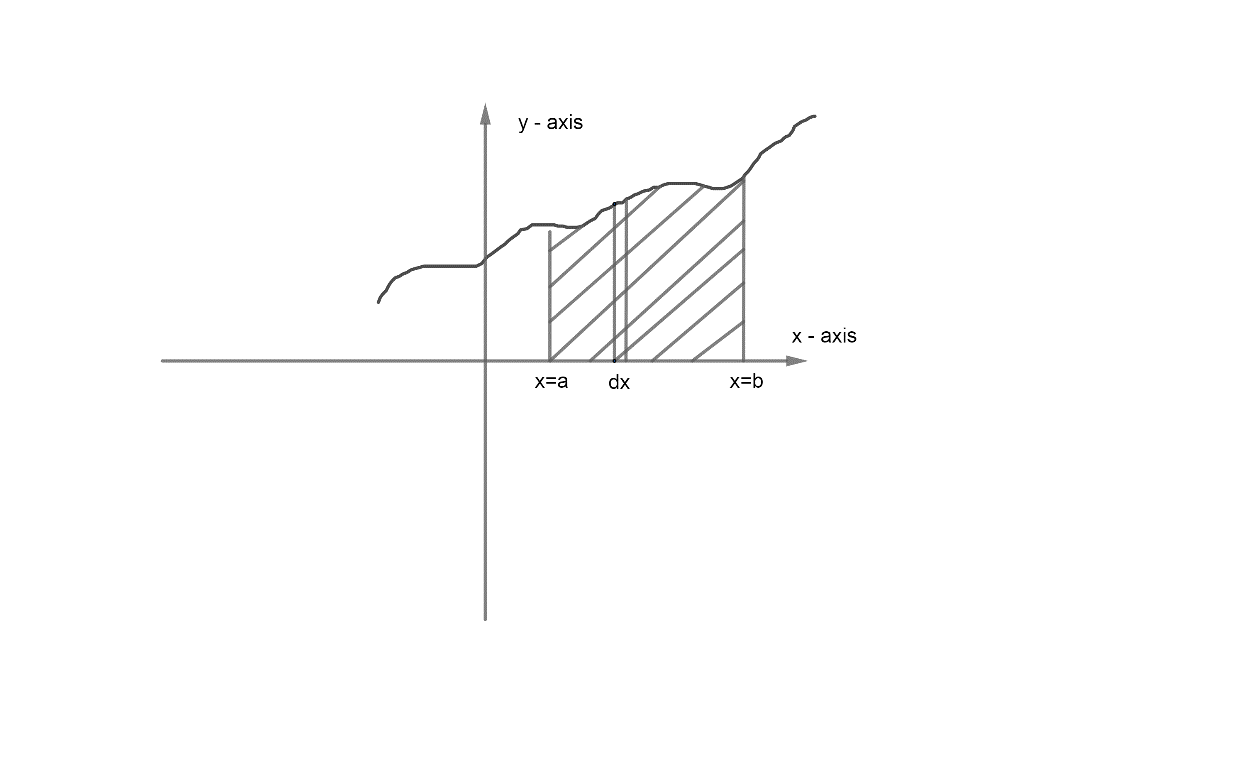
Now, we can see from the graph that $\int\limits_{a}^{b}{f\left( x \right)dx}$ is nothing but the area bounded by the line $y=f\left( x \right),x=a,x=b\ and\ x-axis$.
Now, we have the graph of lines $y=4x+5,x+y=5\ and\ 4y=x+5$ as,

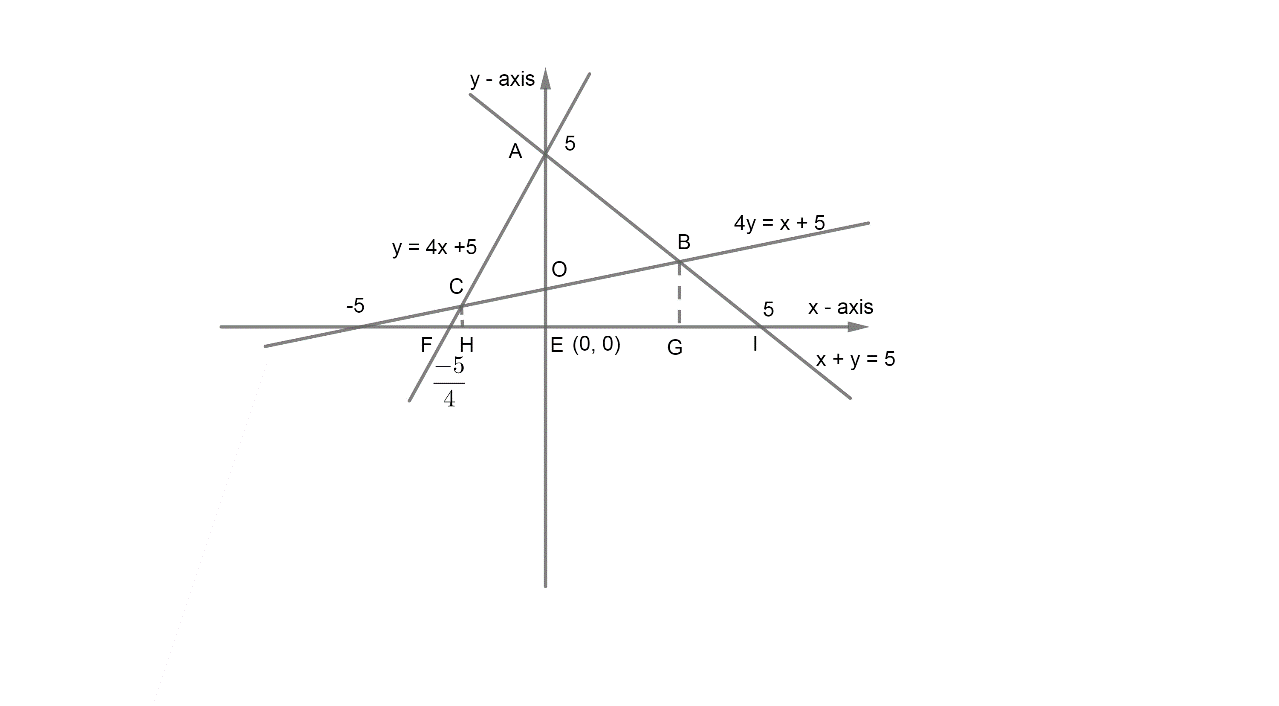
Now, we have the point A as point of intersection of $y=4x+5\ and\ x+y=5$. So, we have,
$\begin{aligned} & 5-x=4x+5 \\\ & 0=5x \\\ & x=0 \\\ \end{aligned}$
Substituting this in $x+y=5$ we have y = 5 and therefore, the point A is (0, 5).
Now, point B is point of intersection of,
$\begin{aligned} & x+y=5.......\left( 1 \right) \\\ & 4y=x+5.......\left( 2 \right) \\\ \end{aligned}$
Now, substituting $x=5-y$ from (1) in (2). We have,
$\begin{aligned} & 4y=5-y+5 \\\ & 5y=10 \\\ & y=2 \\\ \end{aligned}$
Now, we substitute y = 2 in (1). So, we have x = 5 – 2 = 3. Therefore, the point B is (3, 2).
Now, point C is point of intersection of,
$\begin{aligned} & 4y=x+5.......\left( 3 \right) \\\ & y=4x+5.......\left( 4 \right) \\\ \end{aligned}$
So, now we substitute y from (4) in (3).
$\begin{aligned} & \Rightarrow 4\left( 4x+5 \right)=x+5 \\\ & \Rightarrow 16x+20=x+5 \\\ & \Rightarrow 15x=-15 \\\ & \Rightarrow x=-1 \\\ \end{aligned}$
Now, we substitute $x=-1$ in (4). So,
$\begin{aligned} & \Rightarrow y=-4+5 \\\ & \Rightarrow y=1 \\\ \end{aligned}$
Therefore, the point C is (-1, 1).
Now, we will first find the area of $\Delta ACO$. So, we can see that,
$\begin{aligned} & ar\Delta ACO=ar\Delta AFE-arFCOE \\\ & =ar\Delta AFE-ar\Delta FGH-arCHEO \\\ \end{aligned}$
Now, we have to find the x – coordinate of point H and point O which we can see are same as that of point C and point E respectively as -1, 0. So, we have,
$\Rightarrow \int\limits_{\dfrac{-5}{4}}^{0}{\left( 4x+5 \right)dx-\int\limits_{-1}^{0}{\left( \dfrac{x+5}{4} \right)}}dx-\int\limits_{\dfrac{-5}{4}}^{-1}{\left( 4x+5 \right)dx}$
Now, we know that $\int{{{x}^{n}}dx=\dfrac{{{x}^{n+1}}}{n+1}}$. So, we have,
$\begin{aligned} & \Rightarrow 4\dfrac{{{x}^{2}}}{2}+\left. 5x \right|_{\dfrac{-5}{4}}^{0}-\left( \dfrac{{{x}^{2}}}{8}+\dfrac{5}{4}x \right)_{-1}^{0}-\left( 4\dfrac{{{x}^{2}}}{2}+5x \right)_{\dfrac{-5}{4}}^{-1} \\\ & \Rightarrow 2{{\left( \dfrac{-5}{4} \right)}^{2}}+5\left( 0+\dfrac{5}{4} \right)-\left( \dfrac{-{{\left( -1 \right)}^{2}}}{8}+\dfrac{5}{4}\left( 0-\left( -1 \right) \right) \right)-\left( 2\left( {{\left( -1 \right)}^{2}}-{{\left( \dfrac{-5}{4} \right)}^{2}}+ \right)+5\left( -1+\dfrac{5}{4} \right) \right) \\\ & \Rightarrow 2\left( \dfrac{25}{16} \right)+\dfrac{5\times 5}{4}-\left( -\dfrac{1}{8}+\dfrac{5}{4} \right)-\left( 2\left( 1-\dfrac{25}{16} \right)+5\left( \dfrac{5-4}{4} \right) \right) \\\ & \Rightarrow \dfrac{25}{8}+\dfrac{25}{4}-\left( \dfrac{10-1}{8} \right)-\left( 2-\dfrac{25}{8}+\dfrac{5}{4} \right) \\\ & \Rightarrow \dfrac{25+50}{8}-\dfrac{9}{8}-\left( \dfrac{13}{4}-\dfrac{25}{8} \right) \\\ & \Rightarrow \dfrac{75}{8}-\dfrac{9}{8}-\left( \dfrac{26-25}{8} \right) \\\ & \Rightarrow \dfrac{75}{8}-\dfrac{9}{8}-\dfrac{1}{8} \\\ & \Rightarrow \dfrac{75-10}{8} \\\ & \Rightarrow \dfrac{65}{8}sq\ units \\\ \end{aligned}$
Now, similarly we have the area as,
$\begin{aligned} & ar\Delta AOE=ar\Delta AEI-arEOBI \\\ & =ar\Delta AEI-arEOBG-arBGI \\\ & \Rightarrow \int\limits_{0}^{5}{\left( 5-x \right)dx-\int\limits_{0}^{3}{\dfrac{x+5}{4}}}dx-\int\limits_{3}^{5}{\left( 5-x \right)dx} \\\ \end{aligned}$
Now, we know that the area $\int{{{x}^{n}}dx=\dfrac{{{x}^{n+1}}}{n+1}}$. So, we have,
$\begin{aligned} & \Rightarrow \left( 5x-\dfrac{{{x}^{2}}}{2} \right)_{0}^{5}-\dfrac{1}{4}\left( \dfrac{{{x}^{2}}}{2}+5x \right)_{0}^{3}-\left( 5x-\dfrac{{{x}^{2}}}{2} \right)_{3}^{5} \\\ & \Rightarrow \left( 5\left( 5-0 \right)-\dfrac{\left( 25-0 \right)}{2} \right)-\dfrac{1}{4}\left( \dfrac{9-0}{2}+5\left( 3-0 \right) \right)-\left( 5\left( 5-3 \right)-\left( \dfrac{25-9}{2} \right) \right) \\\ & \Rightarrow \left( 25-\dfrac{25}{2} \right)-\dfrac{1}{4}\left( \dfrac{9}{2}+15 \right)-\left( 10-8 \right) \\\ & \Rightarrow \dfrac{25}{2}-\dfrac{1}{4}\left( \dfrac{39}{2} \right)-2 \\\ & \Rightarrow \dfrac{25}{2}-\dfrac{39}{8}-2 \\\ & \Rightarrow \dfrac{100-39-16}{8} \\\ & \Rightarrow \dfrac{100-55}{8} \\\ & \Rightarrow \dfrac{45}{8}sq\ units \\\ \end{aligned}$
Therefore, the area of bounded region is,
$\begin{aligned} & ar\Delta ACO+ar\Delta AOB \\\ & \Rightarrow \dfrac{65+45}{8} \\\ & \Rightarrow \dfrac{110}{8} \\\ & \Rightarrow \dfrac{55}{4}sq\ units \\\ \end{aligned}$
Therefore, the area of the bounded region is $\dfrac{55}{4}sq\ units$.

Note: While solving the question it is important to note that we have used the x – coordinate of G as limit and since the x – coordinate of G is same as that of B. Therefore, we have used the x – coordinate of B for substituting the limit while finding the area of $\Delta AOB$.