Question

Using integration, find the area enclosed by the parabola ${{y}^{2}}=4ax$ and the chord y = mx.

Answer 1

- Hint: First, from the given expression / conditions, find the 2 curves which we need to find the area. Next by using elimination method find the points of intersection of the curves. By looking at their equations, use normal co – ordinate geometry knowledge to find their shapes. Draw the curves together on a graph. By using their diagrams mark the area which is common in both of them. Now, integrate the curves to find the areas and subtract the extra area to get the area which is common to both curves.

Complete step-by-step solution -

Elimination method:
First write 2 curve equations which you need to solve to find intersection points. Then try to convert one variable in terms of another variable by using any one of the equations. Now substitute this variable in terms of others into the remaining equation. Now the remaining equation turns into an equation of one variable.
By normal geometry find the variable. Using previous relations, find the other variable. Thus, you get the intersection point(s).
Chord of a parabola: - The line segments whose endpoints always lie on the parabola is known as a chord. Here it is given y = mx. So, the line passes through origin.
As we know by definition the other end must lie on parabola.
Given expressions in the question are written as: -
\Rightarrow $$$${{y}^{2}}=4ax - (1)
$\Rightarrow y=mx$ - (2)
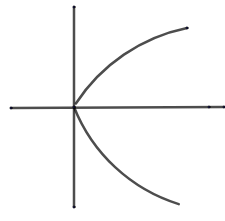
By basic knowledge of geometry we can say ${{y}^{2}}=4ax$ is a parabola sideward with vertex at origin (0, 0) and we can also say y = mx is a straight line through origin.
By substituting equation (2) in equation (1), we get an equation:
$\Rightarrow {{\left( mx \right)}^{2}}=4ax$
By subtracting 4ax on both sides, we get:
$\Rightarrow {{m}^{2}}{{x}^{2}}-4ax=0$
By taking ${{m}^{2}},{{x}^{2}}$ common from equation, we get:
$\Rightarrow {{m}^{2}}x\left( x-\dfrac{4a}{{{m}^{2}}} \right)=0$
Now we take an valid assumption which is ${{m}^{2}}\ne 0$ because as the line is chord it must cut parabola at some other point, but if m = 0 it is cutting parabola only at origin.
So, $m\ne 0$ by this we can say ${{m}^{2}}\ne 0$.
So, by dividing with ${{m}^{2}}$ on both sides, we get:
$\Rightarrow x\left( x-\dfrac{4a}{{{m}^{2}}} \right)=0$
So, roots of above equation, x = 0, x = $\dfrac{4a}{{{m}^{2}}}$.
By substituting these values into equation (2), we get:
If x = 0, y = m (0) = 0 $\Rightarrow$ y = 0.
If x = $\dfrac{4a}{{{m}^{2}}}$, $y=m\left( \dfrac{4a}{{{m}^{2}}} \right)=\dfrac{4a}{m}\Rightarrow y=\dfrac{4a}{m}$.
So, the intersection points are (0, 0) $\left( \dfrac{4a}{{{m}^{2}}},\dfrac{4a}{m} \right)$.
Curves: -
${{y}^{2}}=4ax$

y = mx

Combining: -

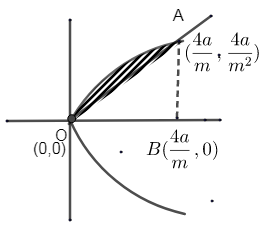
The required area is the difference between the areas of parabola and the straight line from O to A.
So, we will find the both areas separately in the following cases as shown.
Case 1: Area of parabola from O to A. Let it be P.
Area of a curve f (x) as x varies from ${{x}_{1}}$ to ${{x}_{2}}$ is given by
$\Rightarrow A=\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{f\left( x \right)dx}$
Parabola is given as: ${{y}^{2}}=4ax$
By applying square root on both sides, we get:
$\Rightarrow y=\sqrt{4ax}=f\left( x \right)$
We know, ${{x}_{1}}$ = 0 as origin (0, 0), ${{x}_{2}}=\dfrac{4a}{{{m}^{2}}}$ as A $\left( \dfrac{4a}{{{m}^{2}}},\dfrac{4a}{m} \right)$.
So, the area of parabola, P can be written as:
$P=\int\limits_{0}^{\dfrac{4a}{{{m}^{2}}}}{\sqrt{4ax}dx}$
By basic integration we know that, $\int{\sqrt{kx}}=\sqrt{k}\dfrac{{{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}}+C$.
By using this we can write, P in terms of “a” as:
$\Rightarrow P=\left[ \sqrt{4a}{{x}^{\dfrac{3}{2}}}\times \dfrac{2}{3} \right]_{0}^{\dfrac{4a}{{{m}^{2}}}}$
By substituting limits, we get “P” as:
$\Rightarrow P=\sqrt{4a}{{\left( \dfrac{4a}{{{m}^{2}}} \right)}^{\dfrac{3}{2}}}\times \dfrac{2}{3}=\dfrac{16{{a}^{2}}}{{{m}^{3}}}\times \dfrac{2}{3}=\dfrac{32{{a}^{2}}}{3{{m}^{3}}}$
Case 2: Area of straight line from O to A. Let it be Q.
Area of curve f (c) as x varies from ${{x}_{1}}$ to ${{x}_{2}}$ is given by
$\Rightarrow A=\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{f\left( x \right)dx}$
Straight line: - y = mx = f (x). We know ${{x}_{1}}$ = 0 as (0, 0) ${{x}_{2}}=\dfrac{4a}{{{m}^{2}}}$ as A $\left( \dfrac{4a}{{{m}^{2}}},\dfrac{4a}{m} \right)$.
By substituting these Q can be written as:
$\Rightarrow Q=\int\limits_{0}^{\dfrac{4a}{{{m}^{2}}}}{mxdx}$
We know, $\int{xdx}=\dfrac{{{x}^{2}}}{2}+C$
By using above we can write the Q as:
$\Rightarrow Q=\left[ m\dfrac{{{x}^{2}}}{2} \right]_{0}^{\dfrac{4a}{{{m}^{2}}}}$
By substituting limits, we get Q in terms of a as:
$\Rightarrow Q=m{{\left( \dfrac{4a}{{{m}^{2}}} \right)}^{2}}\dfrac{1}{2}-0$
Finally we can write Q in terms of a, m as:
$\Rightarrow Q=\dfrac{8{{a}^{2}}}{{{m}^{3}}}$
Required area is the difference between these 2 areas. So, we can write it as follows:
Required area = P – Q
By substituting P, Q values, we get area as:
Required area $=\dfrac{32{{a}^{2}}}{3{{m}^{3}}}-\dfrac{8{{a}^{2}}}{{{m}^{3}}}$
By taking LCM we can write it as: - Area = $\dfrac{8{{a}^{2}}}{3{{m}^{3}}}$
Therefore the area bounded between given curves is $\dfrac{8{{a}^{2}}}{3{{m}^{3}}}$ square units.

Note: The idea of proving $m\ne 0$ is very cervical because if m = 0 the area bounded can be said to be infinite or zero. Be careful while calculating P. Do not forget the term $\dfrac{2}{3}$, generally students forget to write it. Instead of integration as you know x, y coordinate intersection you can write it as base and height respectively. Use area of triangle for straight lines area calculation.