Question

Using Huygen’s wave theory, derive Snell’s law of refraction.

Answer 1

Snell’s law is explained by the laws of reflection and refraction of light at an interface. Wave theory of light was introduced by Christian Huygens. According to Snell’s law the ratio of sine of angle of incidence to the sine of angle of refraction is equal to the ratio of refractive index of second medium to the first medium.

Complete step by step answer:

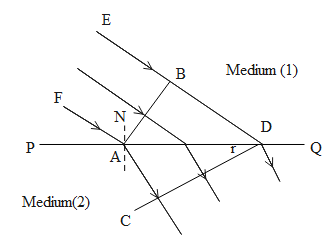
Consider a plane wave front AB incident on the surface PQ separating those two media named 1 and 2.
Let the medium 1 is a rarer medium of refractive index ${{n}_{1}}$ in which light travels with a velocity ${{c}_{1}}$ ​. The medium 2 is denser medium of refractive index ${{n}_{2}}$ ​ in which light travels with a velocity ${{c}_{2}}$.
The angle between the incident ray FA and the normal NA at the point of incidence A is the angle of incidence..
The angle between the incident plane is also equal to the angle between wave front BA and the surface of separation PQ.
So $\angle BAD$ is the angle of incidence of the incident plane wave front AB.
Like this, the angle between the wave front which is refracted and the surface of separation PQ is equal to the angle of refraction r.
That is, $\angle ADC=r$ .
Consider the triangles BAD and ACD figure above.
The sine of the angle BAD can be found by taking the ratio between the opposite sides to the adjacent side.
That is,
$\sin i=\sin \angle BAD$ $=\dfrac{BD}{AD}=\dfrac{{{c}_{1}}r}{AD}$ ……… (1)
Similarly,
$\sin r=\sin \angle ADC$ =$\dfrac{AC}{AD}=\dfrac{{{c}_{2}}r}{AD}$ ……… (2)
Dividing equation (2) by equation (1),
$\dfrac{\sin i}{\sin r}=\dfrac{{{c}_{1}}}{{{c}_{2}}}$
This is the refractive index of the second medium (2) with respect to the first medium (1).
$\dfrac{{{c}_{1}}}{{{c}_{2}}}=\dfrac{{{n}_{2}}}{{{n}_{1}}}$
$\therefore \dfrac{\sin i}{\sin r}=\dfrac{{{n}_{2}}}{{{n}_{1}}}$
This equation proves Snell's law.

Note: According to Snell’s law the ratio of sine of angle of incidence to the sine of angle of refraction is equal to the ratio of refractive index of second medium to the first medium. Huygen’s principle tells us that each point on a wavefront is a source of secondary waves, which add up to later wavefronts. When the speed of light is independent of direction, the secondary waves are spherical.