Question

Using definite integral, compute the area of the region bounded by the sides of the triangle whose vertices are (2, 0), (4, 5) and (6, 3).
(a) 6 square units
(b) 7 square units
(c) 8 square units
(d) 9 square units

Answer 1

To get the area of the triangle with the vertices given we will start with finding the equations of the line of the triangles. We then try to transform the equations in forms of y to use the limits in form of x. Finding the integration of the form of the definite integral gives us our desired result.

Complete step by step solution:
Let us consider A (2, 0), B (4, 5) and C (6, 3) be the vertices of the given triangle.
So, the equation of AB is:
$y - 0 = \dfrac{{5 - 0}}{{4 - 2}}(x - 2)$
$\Rightarrow y = \dfrac{5}{2}(x - 2)$…….. (1)
And, again, the equation of BC is:
$y - 5 = \dfrac{{3 - 5}}{{6 - 4}}(x - 4)$
$\Rightarrow y - 5 = \dfrac{{ - 2}}{2}(x - 4)$
$\Rightarrow y - 5 = - 1(x - 4)$
$\Rightarrow y - 5 = - x + 4$
$\Rightarrow y = 9 - x$……….. (2)
And, the equation of CA is:
$y - 3 = \dfrac{{0 - 3}}{{2 - 6}}(x - 6)$
$\Rightarrow y - 3 = \dfrac{{ - 3}}{{ - 4}}(x - 6)$
$\Rightarrow y - 3 = \dfrac{3}{4}(x - 6)$
Now, by more simplification,
$\Rightarrow 4y - 12 = 3x - 18$
$\Rightarrow y = \dfrac{1}{4}(3x - 6)$
${ \Rightarrow 4y = 3x - 6}$
$\Rightarrow y = \dfrac{3}{4}(x - 2)$………. (3)

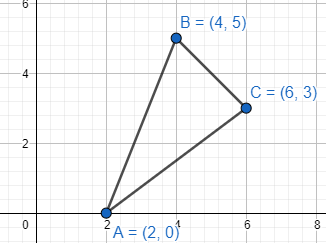
To find the area of the triangle, we are to use the definite integral in this question. Now, we have considered the lines as the forms of “y”. So, we are to integrate the equations with the limits of x. And, if we get the integration with respect to two lines, the third line will be a common part. We have to subtract the integration of the third line with the sum of the other two to find the area.
Now, Area would be,
$\dfrac{5}{2}\int\limits_2^4 {(x - 2)} + \int\limits_4^6 {(9 - x)} - \dfrac{3}{4}\int\limits_4^6 {(x - 2)}$
$= \dfrac{5}{2}\left. {\left( {\dfrac{{{x^2}}}{2} - 2x} \right)} \right|_2^4 + \left. {\left( {9x - \dfrac{{{x^2}}}{2}} \right)} \right|_4^6 - \dfrac{3}{4}\left. {\left( {\dfrac{{{x^2}}}{2} - 2x} \right)} \right|_2^6$
$= \dfrac{5}{2}[6 - 4] + [18 - 10] - \dfrac{3}{4}[16 - 8]$
$= \dfrac{5}{2}.2 + 8 - \dfrac{3}{4}.8$
$= 5 + 8 - 6$
= 7 square units
Hence, the correct option is (b) 7 square units.

Note: We can also solve the problem in a different way. The equations of the lines can be transformed into forms of x to use the limits of y. Using the definite integral with the limits of y gives us our desired result.