Question

Using Bohr's postulates, obtain the expression for the total energy of the electron in the stationary states of the hydrogen atom. Hence draw the energy level diagram showing how the line spectra corresponding to Balmer series occur due to transition energy levels.

Answer 1

According to Bohr's postulates, in a hydrogen atom, a single electron revolves around a nucleus of charge $+ e$. Then the centripetal force is provided by the Coulomb force of gravitational attraction. So,

\dfrac{{m{v^2}}}{r} = \dfrac{{k{e^2}}}{{{r^2}}} \\\ \Rightarrow m{v^2} = \dfrac{{k{e^2}}}{r} \\\ \ $$ In this expression m is the mass of the electron, v is the velocity of the electron and r is the radius of the electron orbit. We can use this information to proceed further. **Complete step by step answer:** From Bohr’s quantization rule, we know that: $mvr = \dfrac{{nh}}{{2\pi }}$ Thus, making velocity the subject of the formula, we have; $ \Rightarrow v = \dfrac{{nh}}{{2\pi mr}}$ Now, we can substitute this value of velocity of electron in the above mathematical expression for centripetal force provided by the gravitational force, we get: $m{\left( {\dfrac{{nh}}{{2\pi mr}}} \right)^2} = \dfrac{{k{e^2}}}{r}$ Solving this mathematical expression for the radius of the electron, we get: $ \Rightarrow r = \dfrac{{{n^2}{h^2}}}{{4\pi mr{e^2}}}$ We can use this value of the radius of the orbit of the electron to obtain the expression for the kinetic energy of the electron. We get: ${E_k} = \dfrac{{k{e^2}4{\pi ^2}km{e^2}}}{{2{n^2}{h^2}}} = \dfrac{{2{\pi ^2}{k^2}m{e^4}}}{{{n^2}{h^2}}}$ Now, similarly we can also obtain the mathematical expression for the potential energy of the electron as well: $\ {E_p} = - \dfrac{{k{e^2}}}{r} = - k{e^2} \times \dfrac{{4{\pi ^2}km{e^2}}}{{{n^2}{h^2}}} \\\ \Rightarrow {E_p} = - \dfrac{{4{\pi ^2}{k^2}m{e^4}}}{{{n^2}{h^2}}} \\\ \ $ Now, we know that the total mechanical energy is equal to the sum of the potential energy and kinetic energy of the particular particle. Thus, we have: $E = {E_p} + {E_k}$ Thus, adding the values for the potential energy and kinetic energy we get: $E = - \dfrac{{2{\pi ^2}{k^2}m{e^4}}}{{{n^2}{h^2}}} = - \dfrac{{13.6}}{{{n^2}}}eV$ Now, we already know that in a Hydrogen atom, when an electron jumps from an orbit with a low energy to an orbit with a high energy, radiation is emitted. The wavelength of this radiation is given by the mathematical expression given below: $\dfrac{1}{\lambda } = R\left( {\dfrac{1}{{n_f^2}} - \dfrac{1}{{n_i^2}}} \right)$ In this mathematical expression, R is the Rydberg constant which is numerically equal to $1.09678 \times {10^{ - 10}}{m^{ - 1}}$ Now, since in the above problem we are only concerned with the Balmer series, we know that for Balmer series; ${n_f} = 2$and ${n_i} = 3,4,5,......$ Putting these values in the mathematical expression given above , we have: $\dfrac{1}{\lambda } = R\left( {\dfrac{1}{{{2^2}}} - \dfrac{1}{{n_i^2}}} \right)$ Calculating this we see that the wavelength of the radiation lies in the visible region of the electromagnetic spectrum. The diagram is represented below: 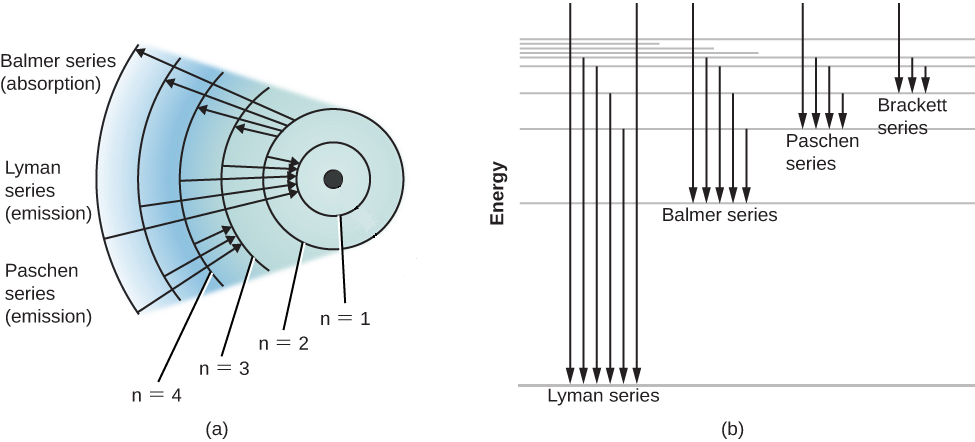 **Note:** Remember that this equation describes emitted light, so the higher energy level is considered the initial level, or ${n_i}$, while the lower level is considered the final level, or ${n_f}$. In the case of the Balmer series, ${n_f}$ is equal to $2$. This equation was combined with the Bohr model to calculate the energy needed to move an electron between its initial and final energy levels.