Question

Using a graph Paper, plot the points $A(6,4)$ and $B(0,4)$ .
A. Reflects A and B in the origin to get the images A’ and B’ .
B. Write the coordinates of A’ and B’ .
C. State the geometrical name of the figure ABA’B’ .
D. Find its Perimeter.

Answer 1

In a point reflection in the origin, the image of the point (x,y) is the point (-x,-y). We will use this to get the points of A’ and B’ then we will join the lines to see which figure is coming forth.

Complete step by step answer:
A.

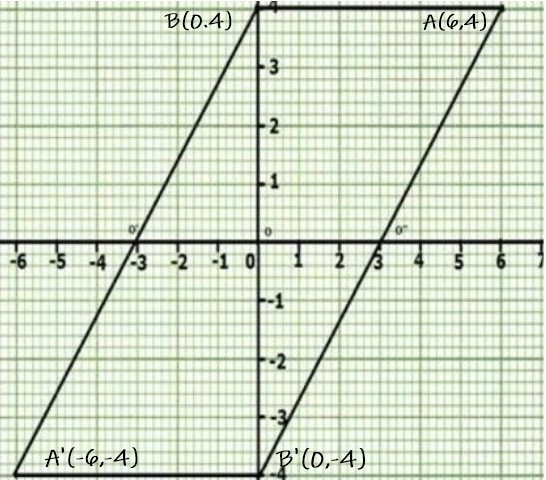
From the Figure and the Hint it is clear that
B. Coordinates of A’ is (-6, -4) and B’ is (0,-4)
C. Also from the figure it is clear that the figure AB A'B’ is actually a parallelogram
D. In the triangle .’ BOO’

OO' = 3units\\\ OB = 4units \end{array}$$ Therefore by pythagoras theorem we will get it as $$\begin{array}{l} BO' = \sqrt {O{B^2} + O'{O^2}} \\\ \Rightarrow BO' = \sqrt {{4^2} + {3^2}} \\\ \Rightarrow BO' = \sqrt {25} \\\ \Rightarrow BO' = 5units \end{array}$$ Since BO’ is 5 units $$BA' = AB = 10 units$$ Which means that the perimeter of ABA’B’ $$ = (6 + 10 + 6 + 10)units = 32units$$ **Note:** Remember that The reflection of the point (x,y) across the x-axis is the point (x,-y), The reflection of the point (x,y) across the y-axis is the point (-x,y) and In a point reflection in the origin, the image of the point (x,y) is the point (-x,-y).