Question

Use Lagrange’s Mean Value Theorem to determine a point on the curve $y=\sqrt{x-2}$ at the tangent that is parallel to the chord joining the points $\left( 2,0 \right)$ and $\left( 3,1 \right)$.

Answer 1

Hint: $y=\sqrt{x-2}$ is an equation of parabola as ${{y}^{2}}=\left( x-2 \right)$. Also, after plotting the graph, we get that $x\in \left( 2,3 \right)$. We will use Lagrange’s Mean Value Theorem or LMVT as, $f'\left( c \right)=\dfrac{f\left( b \right)-f\left( a \right)}{b-a}$ to determine the point.

Complete step-by-step solution -
It is given in the question that we have to use the LMVT to determine a point on the curve $y=\sqrt{x-2}$ at the tangent that is parallel to the chord joining the points $\left( 2,0 \right)$ and $\left( 3,1 \right)$. The given curve $y=\sqrt{x-2}$ is a parabola as ${{y}^{2}}=\left( x-2 \right)$.

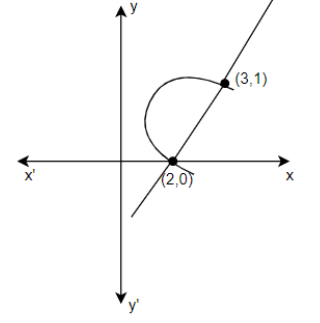
As the coordinates of y are lying between 0 and 1, we are considering the first quadrant. Also, we can see that $x=\left( 2,3 \right)$ from the diagram above. Now, we know that Lagrange’s Mean Value Theorem or LMVT states that if a function $f$ is defined on the closed interval $\left( a,b \right)$, and (i) the function is continuous on the closed interval $\left( a,b \right)$, (ii) and the function $f$ is differentiable on the open interval $\left( a,b \right)$, then there exists a value $x=c$, such that, $f'\left( c \right)=\dfrac{f\left( b \right)-f\left( a \right)}{\left( b-a \right)}$. It means that $f\left( x \right)=\sqrt{x-2}$, where $x\in \left( a,b \right)$. Also, the function is continuous on $\left( 2,3 \right)$. Also, $f'\left( x \right)=\dfrac{1}{2\sqrt{x-2}}$ exists for all $x\in \left( 2,3 \right)$. So, $f\left( x \right)$ is differentiable on $\left( 2,3 \right)$, as $\dfrac{d\sqrt{x}}{dx}=\dfrac{1}{2\sqrt{x}}$.
Thus, both the conditions of the Lagrange’s Mean Value Theorem are satisfied. Also, there must be some $c\in \left( 2,3 \right)$, such that,
$f'\left( c \right)=\dfrac{f\left( b \right)-f\left( a \right)}{\left( b-a \right)}$
So, substituting the values in the above equation, we get,
$f'\left( c \right)=\dfrac{f\left( 3 \right)-f\left( 2 \right)}{\left( 3-2 \right)}$
Now, we know that $f\left( x \right)=\sqrt{x-2}$ and $f'\left( x \right)=\dfrac{1}{2\sqrt{x-2}}$, so we get,
$f\left( 3 \right)=\sqrt{3-2}=1$ and $f\left( 2 \right)=\sqrt{2-2}=0$. So, we get,
$\begin{aligned} & \dfrac{1}{2\sqrt{x-2}}=\dfrac{1-0}{3-2} \\\ & \Rightarrow \dfrac{1}{2\sqrt{x-2}}=1 \\\ \end{aligned}$
Squaring both the sides, we get,
$\dfrac{1}{4\left( x-2 \right)}=1$
Now, by cross multiplying both sides, we get,
$\begin{aligned} & 1=4\left( x-2 \right) \\\ & \Rightarrow 4x-8=1 \\\ & \Rightarrow 4x=9 \\\ & \Rightarrow x=\dfrac{9}{4} \\\ \end{aligned}$
So, the value of $c=\dfrac{9}{4}$, when $f\left( 2,3 \right)$.
Therefore $\dfrac{9}{4}$ is a point on the curve $y=\sqrt{x-2}$ such that the tangent is parallel to the chord joining the points $\left( 2,0 \right)$ and $\left( 3,1 \right)$.

Note: The students should check before applying the Lagrange’s Mean Value Theorem, if the function satisfies all the necessary conditions such as, (i) the function is continuous on $\left( a,b \right)$, (ii) and the function f is differentiable on $\left( a,b \right)$. We should apply LMVT only if it satisfies the conditions, but usually the students do not check these conditions and end up with the wrong answer.