Question

Use Kirchhoff’s rules to obtain the balance condition in a Wheatstone bridge.

Answer 1

There are two rules of Kirchhoff: The first rule is called junction rule, it states that the sum of all currents entering a junction must be equal to the sum of all currents leaving the junction. Kirchhoff’s second rule is called the loop rule, it states that the algebraic sum of all potential around any closed circuit should be zero.

Complete step by step solution:
As per Kirchhoff’s first rule, it can be mathematically expressed as:
$\Sigma i =0$
Where $\Sigma i$ is the sum of current entering the junction and current leaving the junction.
As per Kirchhoff’s second rule, it can be expressed as:
$\Sigma iR=\Sigma E$
Where $\Sigma R$ is the resistance at the junction and $\Sigma E$ is the emf at the junction.
The circuit diagram for Wheatstone bridge is as follows:

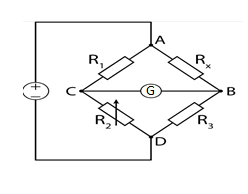
Here G is the galvanometer and it is used to measure the current flowing across two points.
And ${{R}_{1}},{{R}_{2}},{{R}_{3\,}}\,and\,{{R}_{x}}$ are the resistances connected as shown in the above diagram.
The resistances are connected across the points C and D as shown. When the current is flown through the circuit and the galvanometer does not give any deflection, then the bridge is balanced. For balanced bridge we must have the condition as:
$\dfrac{{{R}_{x}}}{{{R}_{3}}}=\dfrac{{{R}_{1}}}{{{R}_{2}}}$
Let the total current flowing in the circuit be I. Now this current is divided into two parts i1​ and i2 flowing through ${{R}_{x}}\,,{{R}_{3}}\,and\,{{R}_{1\,}},{{R}_{2}}$ . When the Wheatstone is balanced, the galvanometer shows zero deflection, that is the potential of B and C will be equal. In the closed circuit ABCD, by Kirchhoff’s second law, we will have:
$\Rightarrow {{i}_{1}}{{R}_{1}}-{{i}_{2}}{{R}_{x}}=0$
$\Rightarrow {{i}_{1}}{{R}_{1}}={{i}_{2}}{{R}_{x}}$ --equation 1
And
${{i}_{1}}{{R}_{2}}-{{i}_{2}}{{R}_{3}}=0$
$\Rightarrow {{i}_{1}}{{R}_{2}}={{i}_{2}}{{R}_{3}}$ --equation 2
Dividing equation 1 by equation 2, we have
$\dfrac{{{i}_{1}}{{R}_{1}}}{{{i}_{1}}{{R}_{2}}}=\dfrac{{{i}_{2}}{{R}_{x}}}{{{i}_{2}}{{R}_{3}}}$
$\therefore \dfrac{{{R}_{1}}}{{{R}_{2}}}=\dfrac{{{R}_{x}}}{{{R}_{3}}}$
Which is the required condition.

Note: Remember that there are two rules of Kirchhoff’s law. The condition for balanced Wheatstone can be obtained using both the rules. Kirchhoff’s laws are used to study any type of circuit whether simple or complex circuit.