Solveeit Logo
Login

Question

Question: Use Kirchhoff’s rules to determine the value of current \({I_1}\)flowing in the circuit shown in the...

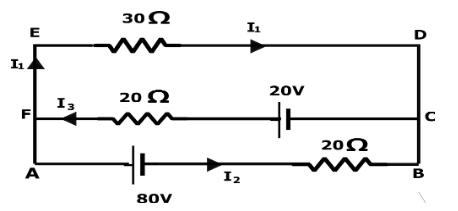
Use Kirchhoff’s rules to determine the value of current I1{I_1}flowing in the circuit shown in the figure.

Explanation

Solution

We can see how the Kirchhoff’s law is applied on the circuit keeping in mind all the sign conventions to form the equations. After applying the laws we will get some equations and on solving those, we can get the required value of current.We can use both the methods of substitution and elimination to solve the equations.

Complete step by step answer:
Kirchhoff’s two laws can be used to determine the required value of current.
Current law: The total current entering a node (coming towards it) is always equal to the total current leaving so that the loss is zero.The sum of currents at the junction is zero.
Sign convention: The current facing towards the node is taken as positive and away from it as negative.
For the shown diagram the equation becomes:

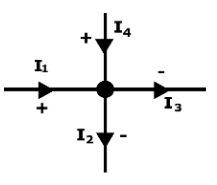
I1−I2−I3+I4=0 ⇒I1+I4=I2+I3  {I_1} - {I_2} - {I_3} + {I_4} = 0 \\\ \Rightarrow {I_1} + {I_4} = {I_2} + {I_3} \\\
Voltage law: In a closed loop the sum of potential of the circuit involving resistors is zero. We also consider the product of current and resistance because according to ohm’s law V = IR.
Sign convention: while moving in a loop, if the negative terminal of a cell comes first, then the voltage will be taken as negative and vice – versa.If the direction of current in the arm is the same as the path of the loop we are following, then the product of current and resistor is positive, otherwise negative.
For moving in loop PQRS in the shown figure, the equation becomes:

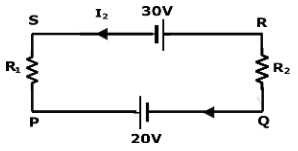
20−I1R2+30+I2R1=0 ⇒I2R1−I1R2=−50  20 - {I_1}{R_2} + 30 + {I_2}{R_1} = 0 \\\ \Rightarrow {I_2}{R_1} - {I_1}{R_2} = - 50 \\\
Now, applying Kirchhoff’s laws on the given circuit:
According to Kirchhoff’s law on the node F:
I3−I1−I2=0 ⇒I3=I1+I2......(1)  {I_3} - {I_1} - {I_2} = 0 \\\ \Rightarrow {I_3} = {I_1} + {I_2}......(1) \\\
According to Kirchhoff’s law in the loop CBAF:

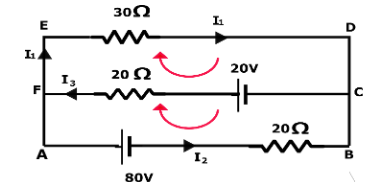
\-I2×20+80−I3×20+20=0 ⇒−20I2−20I3+100=0 ⇒20I2+20I3=100 ⇒I2+I3=5...(2)  \- {I_2} \times 20 + 80 - {I_3} \times 20 + 20 = 0 \\\ \Rightarrow - 20{I_2} - 20{I_3} + 100 = 0 \\\ \Rightarrow 20{I_2} + 20{I_3} = 100 \\\ \Rightarrow {I_2} + {I_3} = 5...(2) \\\
According to Kirchhoff’s law in the loop CFED:
\-20+I3×20+I1×30=0 ⇒20I3+30I1=20 ⇒2I3+3I1=2......(3)  \- 20 + {I_3} \times 20 + {I_1} \times 30 = 0 \\\ \Rightarrow 20{I_3} + 30{I_1} = 20 \\\ \Rightarrow 2{I_3} + 3{I_1} = 2......(3) \\\
Using the obtained three equations, we will find the value of I1{I_1}.
Substituting value of I3{I_3} from (1) in (2). It becomes:
I2+I1+I2=5 ⇒I1+2I2=5....(4)  {I_2} + {I_1} + {I_2} = 5 \\\ \Rightarrow{I_1} + 2{I_2} = 5....(4) \\\
Substituting this value of I3{I_3} from (1) in (3). It becomes:
2I1+2I2+3I1=2 ⇒5I1+2I2=2....(5)  2{I_1} + 2{I_2} + 3{I_1} = 2 \\\ \Rightarrow5{I_1} + 2{I_2} = 2....(5) \\\
Subtracting (4) from (5), we get:

4I1=−3 ⇒I1=−34 ∴I1=−0.75A4{I_1} = - 3 \\\ \Rightarrow {I_1} = - \dfrac{3}{4}\\\ \therefore {I_1}= -0.75 A

Therefore the magnitude of the current flowing in the circuit is 0.75 A.

Note: The current law is called the first Kirchhoff’s law and is applicable to both open and closed circuits.The voltage law is called the second Kirchhoff’s law and is applicable only to closed circuits. The rules in terms of algebraic sum can be written as
Current: ∑I=0\sum I = 0
Voltage: ∑V+∑IR=0\sum {V + \sum {IR} = 0}
The current law proposed by Kirchhoff is in accordance with the conservation of charge and the voltage law is in accordance with the conservation of energy.