Question

Use Euler's method to solve the equation $\frac{dy}{dx}=1+xy$ with $y(0) = 1$ and tabulate the solution for $x = 0$ to $x = 0.4$. Take $h = 0.1$ and correct the solution upto fourth decimal place.

Answer 1

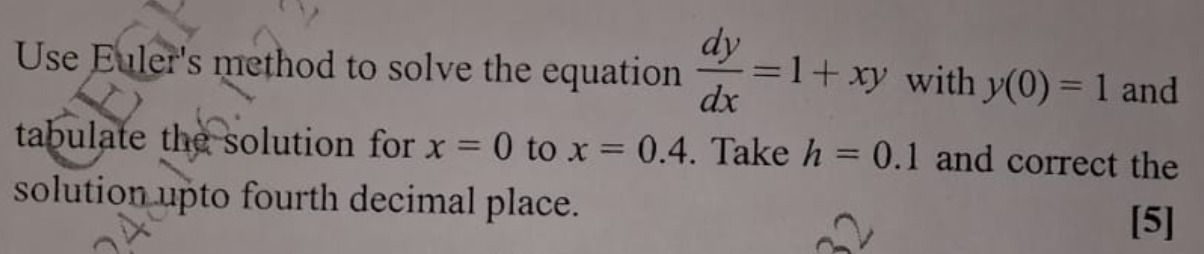
The tabulated solution using Euler's method is:

$x$	$y$
0.0	1.0000
0.1	1.1000
0.2	1.2110
0.3	1.3352
0.4	1.4753

Answer 2

The given differential equation is $\frac{dy}{dx} = f(x, y) = 1 + xy$, with the initial condition $y(0) = 1$. The step size is $h = 0.1$. We use Euler's method formula: $y_{n+1} = y_n + h f(x_n, y_n)$. We start with $(x_0, y_0) = (0, 1)$ and iterate to find $y$ values for $x = 0.1, 0.2, 0.3, 0.4$.

1. For $n=0$: $x_0 = 0$, $y_0 = 1.0000$ $f(x_0, y_0) = 1 + (0)(1) = 1.0000$ $y_1 = y_0 + h f(x_0, y_0) = 1.0000 + 0.1 \times 1.0000 = 1.1000$ $x_1 = x_0 + h = 0.1$

2. For $n=1$: $x_1 = 0.1$, $y_1 = 1.1000$ $f(x_1, y_1) = 1 + (0.1)(1.1000) = 1 + 0.1100 = 1.1100$ $y_2 = y_1 + h f(x_1, y_1) = 1.1000 + 0.1 \times 1.1100 = 1.1000 + 0.1110 = 1.2110$ $x_2 = x_1 + h = 0.2$

3. For $n=2$: $x_2 = 0.2$, $y_2 = 1.2110$ $f(x_2, y_2) = 1 + (0.2)(1.2110) = 1 + 0.2422 = 1.2422$ $y_3 = y_2 + h f(x_2, y_2) = 1.2110 + 0.1 \times 1.2422 = 1.2110 + 0.12422 = 1.33522$ Rounding to four decimal places: $y_3 \approx 1.3352$ $x_3 = x_2 + h = 0.3$

4. For $n=3$: $x_3 = 0.3$, $y_3 = 1.3352$ $f(x_3, y_3) = 1 + (0.3)(1.3352) = 1 + 0.40056 = 1.40056$ $y_4 = y_3 + h f(x_3, y_3) = 1.3352 + 0.1 \times 1.40056 = 1.3352 + 0.140056 = 1.475256$ Rounding to four decimal places: $y_4 \approx 1.4753$ $x_4 = x_3 + h = 0.4$