Question

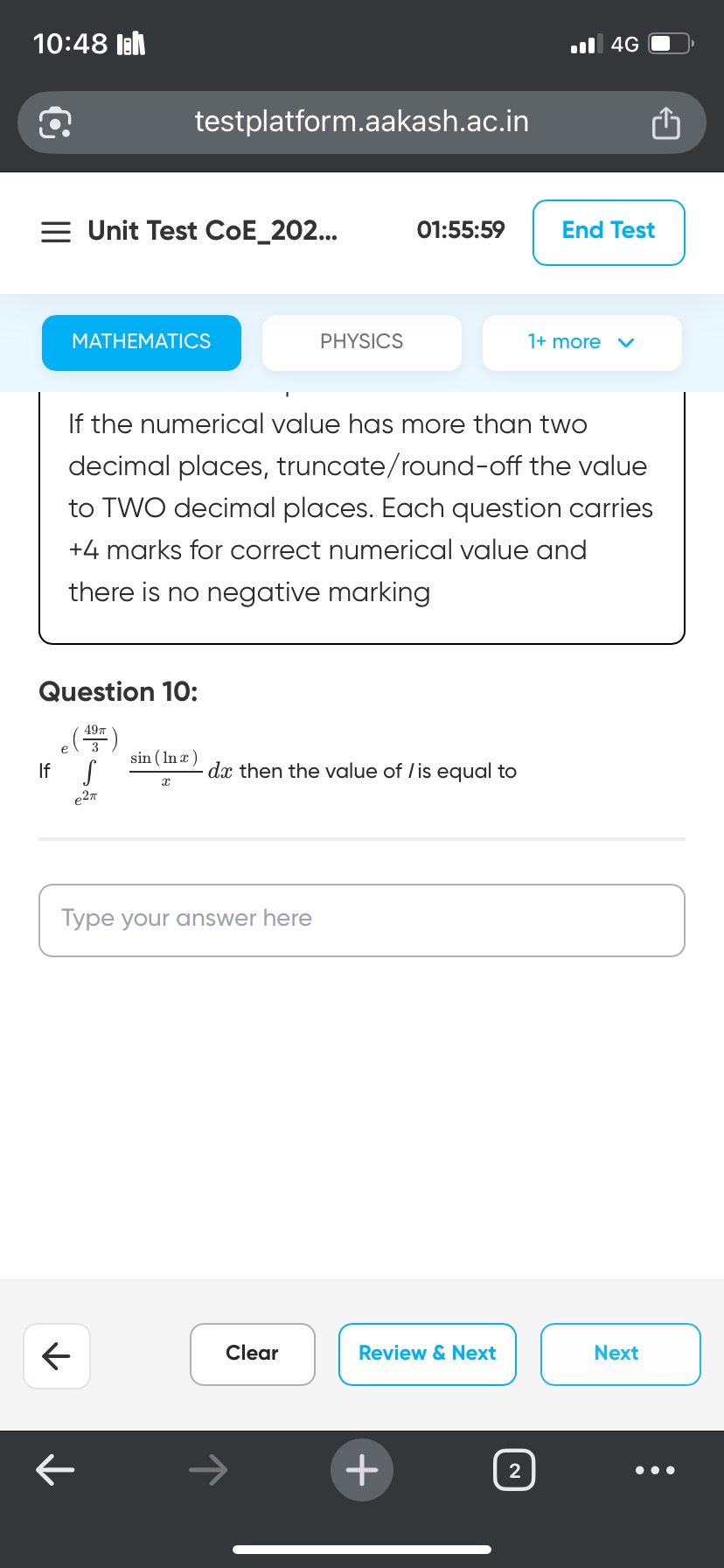
If $\int_{e^{2\pi}}^{e^{\frac{49\pi}{3}}} \frac{sin(lnx)}{x} dx$ then the value of $I$ is equal to

Answer 1

0.50

Answer 2

To evaluate the integral $I = \int_{e^{2\pi}}^{e^{\frac{49\pi}{3}}} \frac{\sin(\ln x)}{x} dx$, we use the method of substitution.

1. Substitution: Let $u = \ln x$.
Differentiating both sides with respect to $x$:
$\frac{du}{dx} = \frac{1}{x}$
So, $du = \frac{1}{x} dx$.

2. Change of Limits: When $x = e^{2\pi}$:
$u_1 = \ln(e^{2\pi}) = 2\pi$

When $x = e^{\frac{49\pi}{3}}$:
$u_2 = \ln(e^{\frac{49\pi}{3}}) = \frac{49\pi}{3}$

3. Rewrite the Integral: Substitute $u$ and $du$ into the integral with the new limits:
$I = \int_{2\pi}^{\frac{49\pi}{3}} \sin(u) du$

4. Integrate: The integral of $\sin(u)$ is $-\cos(u)$.
$I = [-\cos(u)]_{2\pi}^{\frac{49\pi}{3}}$

5. Apply the Limits: $I = -\cos\left(\frac{49\pi}{3}\right) - (-\cos(2\pi))$
$I = -\cos\left(\frac{49\pi}{3}\right) + \cos(2\pi)$

6. Evaluate Trigonometric Terms: We know that $\cos(2\pi) = 1$.
For $\cos\left(\frac{49\pi}{3}\right)$, we can rewrite the angle:
$\frac{49\pi}{3} = \frac{48\pi + \pi}{3} = 16\pi + \frac{\pi}{3}$
Since the cosine function has a period of $2\pi$, $\cos(2n\pi + \theta) = \cos(\theta)$ for any integer $n$.
Therefore, $\cos\left(16\pi + \frac{\pi}{3}\right) = \cos\left(\frac{\pi}{3}\right)$.
We know that $\cos\left(\frac{\pi}{3}\right) = \frac{1}{2}$.

7. Calculate the Value of I: Substitute these values back into the expression for $I$:
$I = -\frac{1}{2} + 1$
$I = \frac{1}{2}$

8. Round-off to Two Decimal Places: The numerical value is $\frac{1}{2} = 0.5$.
To two decimal places, this is $0.50$.