Question

Uniformly charged long cylinder has volume charge density$\rho$. Find an electric field at a distance$x < R$from the axis of the cylinder.
(A) $\dfrac{{\rho x}}{{{\varepsilon _0}}}$
(B) $\dfrac{{\rho x}}{{2{\varepsilon _0}}}$
(C) $\dfrac{{\rho x}}{{3{\varepsilon _0}}}$
(D) $\dfrac{{\rho x}}{{4{\varepsilon _0}}}$

Answer 1

For symmetric objects like a cylinder, it is very easy to apply Gauss’s law. In this specific problem, we have given that volume charge density $\rho$ is uniform throughout the cylinder. For calculation, take a cylinder of radius $x$ and then compute the required volume and surface area.

Formula used:
Gauss’s law is given as
$\oint {\overrightarrow E .\overrightarrow {ds} = \dfrac{{{q_e}_n}}{{{\varepsilon _0}}}}$
Where ${q_e}_n$ is the charge enclosed within the Gaussian surface.
$\overrightarrow E$ is the electric field.
$\overrightarrow {ds}$ is the surface area element

Complete step by step solution:
Consider a cylinder of radius $x$ and length $l$.

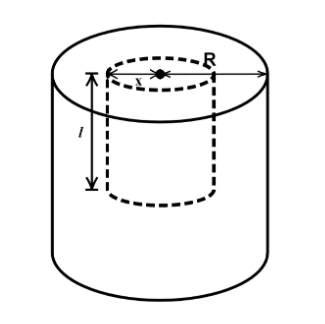
Here, the long cylinder with radius $R$ is shown in a solid line and the Gaussian surface that we have taken with radius $x$and length $l$is shown in the dotted line.
We know that,
$\oint {\overrightarrow E .\overrightarrow {ds} = \dfrac{{{q_e}_n}}{{{\varepsilon _0}}}}$ $- - - - (1)$
Here, we have volume charge density $\rho$and a cylinder (Gaussian surface) of radius$x$and length$l$.
So, the charge enclosed within this cylinder can be calculated as
${q_e}_n = \rho \times V$
Here,$V$is the volume of the cylinder.
$\Rightarrow {q_e}_n = \rho \times \pi {x^2}l$
Using this in the equation$(1)$, we get
$\oint {\overrightarrow E .\overrightarrow {ds} = \dfrac{{\rho \times \pi {x^2}l}}{{{\varepsilon _0}}}}$
Here, the surface area element is
$\overrightarrow {ds} = 2\pi xl$
Using this in the above equation, we get
$E2\pi xl = \dfrac{{\rho \times \pi {x^2}l}}{{{\varepsilon _0}}}$
$\Rightarrow E = \dfrac{{\rho \pi {x^2}l}}{{2\pi xl{\varepsilon _0}}}$
Solving this, we get
$E = \dfrac{{\rho x}}{{2{\varepsilon _0}}}$

Thus, option (B) is correct.

Additional information: While choosing the Gaussian surface, theoretically we can take any shape or size. But while calculating it would be difficult to calculate the surface area or volume of any arbitrary shape. Moreover, if the given charge density is cylindrical, it is suggested to take a cylindrical Gaussian surface. If you have any doubts, you can try to solve this simple question by taking a spherical Gaussian surface.

Note: In this problem, we have been given a constant volume charge density. But if the volume charge density is given like$\rho = {\rho _0}x$, then you simply can’t calculate the enclosed charge like this problem. You have to integrate over the whole volume of your Gaussian surface.