Question

Uniform electric field of magnitude $100V{m^{ - 1}}$ in space is directed along the line $y = 3 + x$. Find the potential difference between point $A\left( {3,1} \right)$ and $B\left( {1,3} \right)$.
A) $100V$
B) $200\sqrt 2 V$
C) $200V$
D) $0$

Answer 1

To solve this question we have to first plot the line $y = 3 + x$ . We can easily find the y-intercept and slope of the lone by comparing it with the standard equation. After that we can convert the electric field into its vector form. Also we have to find the position vector of AB. We can then use the electric field and the position vector to find potential differences.

Formulae used:
$y = mx + c$
Where $y$ is the Y-coordinate, $m$ is the slope of the line, $x$ is the X-coordinate of the line and $c$ is the y-intercept of the line.
$\vec r = \left( {{x_2} - {x_1}} \right)\hat i + \left( {{y_2} - {y_1}} \right)\hat j$
Here $\vec r$ is the position vector and $\left( {{x_1},{y_1}} \right)$and $\left( {{x_2},{y_2}} \right)$are the coordinates of two points.
$V = \vec E.\vec r$
Here $V$ potential difference between two points, $\vec E$ is the electric field vector and $\vec r$ is the position vector.

Complete step by step solution:
In the question equation of a straight line is given.
$y = 3 + x$
Let it be equation 1.
We know that,
$y = mx + c$
Where $y$ is the Y-coordinate, $m$ is the slope of the line, $x$ is the X-coordinate of the line and $c$ is the y-intercept of the line.
Comparing equation 1 with the equation of a straight line, we get
$\Rightarrow m = 1 = \tan 45^\circ$ and
$\Rightarrow c = 3$
Using the above values, we can plot the line

It's said in the question that that electric field is in the direction of the given line.

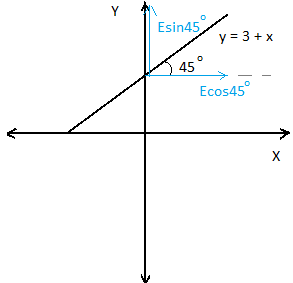
So the components of the electric field will be,
$\Rightarrow \vec E = \left| E \right|\cos 45\hat i + \left| E \right|\sin 45\hat j$
Putting the value of $\left| E \right|$ in the above equation we get,
$\Rightarrow \vec E = 100\cos 45\hat i + 100\sin 45\hat j$
$\Rightarrow \vec E = 100 \times \dfrac{1}{{\sqrt 2 }}\hat i + 100 \times \dfrac{1}{{\sqrt 2 }}\hat j$
$\Rightarrow \vec E = \dfrac{{100}}{{\sqrt 2 }}\hat i + \dfrac{{100}}{{\sqrt 2 }}\hat j$
In the question, it's given that we have found the potential difference between point $A\left( {3,1} \right)$ and $B\left( {1,3} \right)$. So the position vector will be,
$\Rightarrow \vec r = \left( {{x_2} - {x_1}} \right)\hat i + \left( {{y_2} - {y_1}} \right)\hat j$
Here $\vec r$ is the position vector and $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are the coordinates of two given points.
Substituting the value of the coordinates at point $A\left( {3,1} \right)$ and $B\left( {1,3} \right)$ we get,
$\Rightarrow \vec r = \left( {1 - 3} \right)\hat i + \left( {3 - 1} \right)\hat j$
$\Rightarrow \vec r = - 2\hat i + 2\hat j$
So applying the formulae
$\Rightarrow V = \vec E.\vec r$
Where $V$ potential difference between two points, $\vec E$ is the electric field vector and $\vec r$ is the position vector, we get,
$\Rightarrow V = \left( {\dfrac{{100}}{{\sqrt 2 }}\hat i + \dfrac{{100}}{{\sqrt 2 }}} \right).\left( { - 2\hat i + 2\hat j} \right)$
$\Rightarrow V = \left( {\dfrac{{100}}{{\sqrt 2 }} \times - 2} \right) + \left( {\dfrac{{100}}{{\sqrt 2 }} \times 2} \right) = - \dfrac{{200}}{{\sqrt 2 }} + \dfrac{{200}}{{\sqrt 2 }} = 0$
Hence the electric field between the points $A\left( {3,1} \right)$ and $B\left( {1,3} \right)$ will be zero.

Hence option (D) is the correct option.

Note: The electric field can be defined as the gradient of potential difference. It is a vector quantity. So always remember to write it in vector form while solving. Also be careful with the directions. The potential difference also called as voltage is directly proportional to the magnitude of uniform electric field. This is true only for uniform electric fields and if the field was not uniform then this proportionality will not be valid.