Question

Under what condition will the direction of sum and difference of two vectors be the same?

Answer 1

We use vector addition and subtraction to solve this problem. Since the problem is asking us to find the conditions for the same direction and not magnitude, we do not use the formula for vector resultant.

Complete step by step answer:
Let us consider two vectors of different magnitudes acting in the same direction.

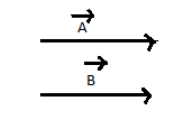
Let us name the first vector as $\vec A$ and the second vectors as $\vec B$
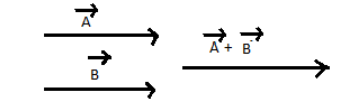
Sum of these vectors will be $\vec A + \vec B$
The direction will be the same as that of both vectors.

Now, the difference between both these vectors is, $\vec A - \vec B$,

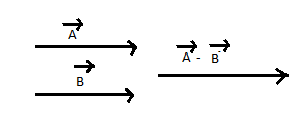
The direction will still be the same as that of the sum of both the vectors. This is because the vector $\vec A$ is greater than $\vec B$. If the vector $\vec B$ was greater then the direction would be the opposite.
If both the vectors were of equal magnitude then the difference in these vectors would give a null vector which has no direction, so the directions of the sum vector and difference vector will be different.
Hence the direction of sum and difference of two vectors will remain the same as long as the two vectors are of different magnitude, acting in the same direction. And the difference should be taken such that the vector with less magnitude should be subtracted from the vector with greater magnitude.
Also, the two vectors shouldn’t be null because null vectors don’t have a direction.

Note: The question asks about the direction of the vectors only. One might get confused with the question if read in a hurry, mistaking direction with magnitude. If the question asked was about magnitude then the resultant vector formula should be used. In this case that is not necessary.