Question

Under what condition does a biconvex lens of glass having a certain refractive index act as a plane glass sheet when immersed in a liquid?

Answer 1

When a lens acts as a plane glass sheet, the angle of incidence and angle of refraction is equal. Thus, use the equation from Snell’s law to get the necessary condition for the refractive index. Light rays pass undeflected only the refractive indices of the lens and the outer medium are equal or the ray passes through the optical center.
Complete step by step solution:

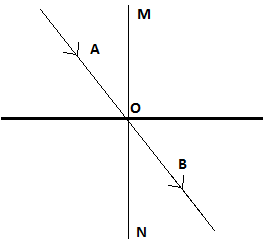
In the above diagram, the ray AOB goes without getting deviated at the interface MN. Thus, $\angle AOM = \angle BON$ since they are opposite angles. They are respectively the angles of incidence and angle of refraction.
Thus, if a lens is placed in a medium and a ray of light passes through the lens without getting deviated, then the angle of incidence and angle of reflection must be the same.
Using Snell’s law of refraction we get
$\mu \sin \theta = const$
${\mu _{medium}}\operatorname{sini} = {\mu _{lens}}\operatorname{sinr}$
Since $i = r$ ,
$\therefore {\mu _{medium}} = {\mu _{lens}}$
Therefore for a biconvex lens of glass having a certain refractive index to act as a plane glass sheet, when immersed in a liquid, the refractive index for both the lens and medium should be the same.

Additional Information:
The change in direction or bending of a light wave passing from one transparent medium to another; caused by the change in wave’s speed is known as “Refraction”. The extent of bending of light rays entering from one medium to another medium is called the “Refractive Index”. It is denoted by $\mu$ . It is represented as $\mu = \dfrac{c}{v}$ . Here $c$ is the speed of light in vacuum and $v$ is the speed of light in medium.

Note: Remember the Snell’s law of refraction. Use in the above problem. Also remember the case when a convex lens would work as a diverging lens. The above problem is a proof that the only case for which the ray of light does not deflect from the initial path is when the refractive indices of both the mediums are equal.