Question

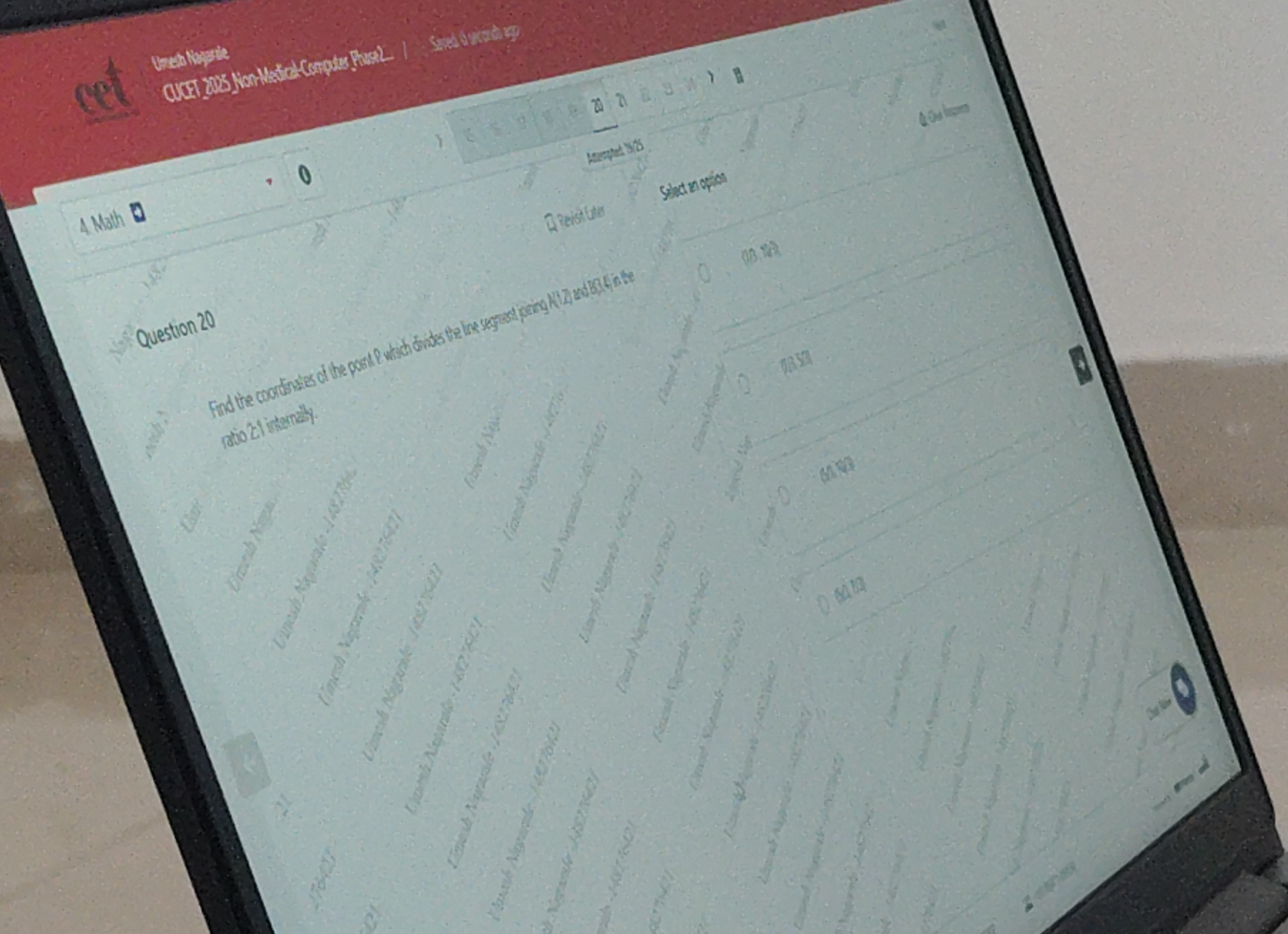
Find the coordinates of the point P which divides the line segment joining A(1,2) and B(3,4) in the ratio 2:1 internally.

• A. (1/3, 10/3)
• B. (7/3, 5/3)
• C. (5/3, 10/3)
• D. (8/3, 11/3)

Answer 1

(7/3, 10/3)

Answer 2

To find the coordinates of point P, we use the section formula for internal division:

$P(x, y) = \left( \frac{m x_2 + n x_1}{m+n}, \frac{m y_2 + n y_1}{m+n} \right)$

Given:

• A($x_1, y_1$) = (1, 2)
• B($x_2, y_2$) = (3, 4)
• Ratio m:n = 2:1

Substitute the values:

$x = \frac{2 \times 3 + 1 \times 1}{2+1} = \frac{7}{3}$

$y = \frac{2 \times 4 + 1 \times 2}{2+1} = \frac{10}{3}$

Therefore, P = $\left( \frac{7}{3}, \frac{10}{3} \right)$. None of the options match, however, the correct answer is $\left( \frac{7}{3}, \frac{10}{3} \right)$.