Question
Question: $\begin{vmatrix} x+1 & 3 & 5\\ 2 & x+2 & 5\\ 2 & 3 & x+4 \end{vmatrix} = 0$, then x will be equal to...
x+1223x+2355x+4=0, then x will be equal to:
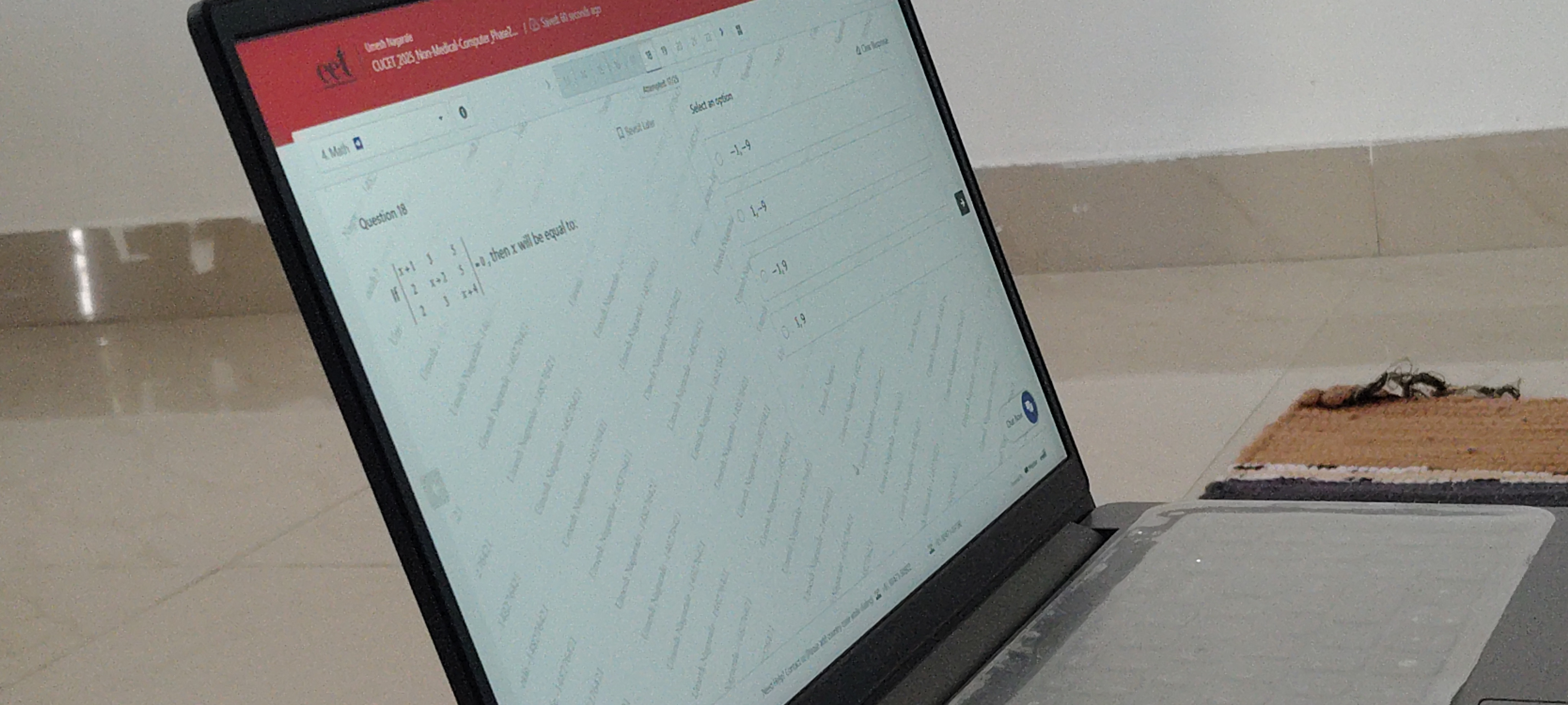
-1,-9
1,-9
-1,9
1,9
1,-9
Solution
To solve the given determinant equation, we will use properties of determinants to simplify it before expansion.
The given equation is: x+1223x+2355x+4=0
Let D denote the determinant.
Step 1: Apply column operation C1→C1+C2+C3
This operation adds the elements of the second and third columns to the first column.
D=(x+1)+3+52+(x+2)+52+3+(x+4)3x+2355x+4
D=x+9x+9x+93x+2355x+4
Step 2: Take (x+9) common from the first column (C1)
D=(x+9)1113x+2355x+4
Step 3: Apply row operations R2→R2−R1 and R3→R3−R1
These operations will create zeros in the first column, making the determinant easier to evaluate.
D=(x+9)11−11−13(x+2)−33−355−5(x+4)−5
D=(x+9)1003x−1050x−1
Step 4: Evaluate the determinant
The resulting matrix is an upper triangular matrix. The determinant of a triangular matrix is the product of its diagonal elements.
D=(x+9)⋅[1⋅(x−1)⋅(x−1)] D=(x+9)(x−1)2
Step 5: Set the determinant to zero and solve for x
Given D=0: (x+9)(x−1)2=0
This equation holds true if either of the factors is zero:
- x+9=0⟹x=−9
- (x−1)2=0⟹x−1=0⟹x=1
Thus, the values of x for which the determinant is zero are 1 and −9.
