Question

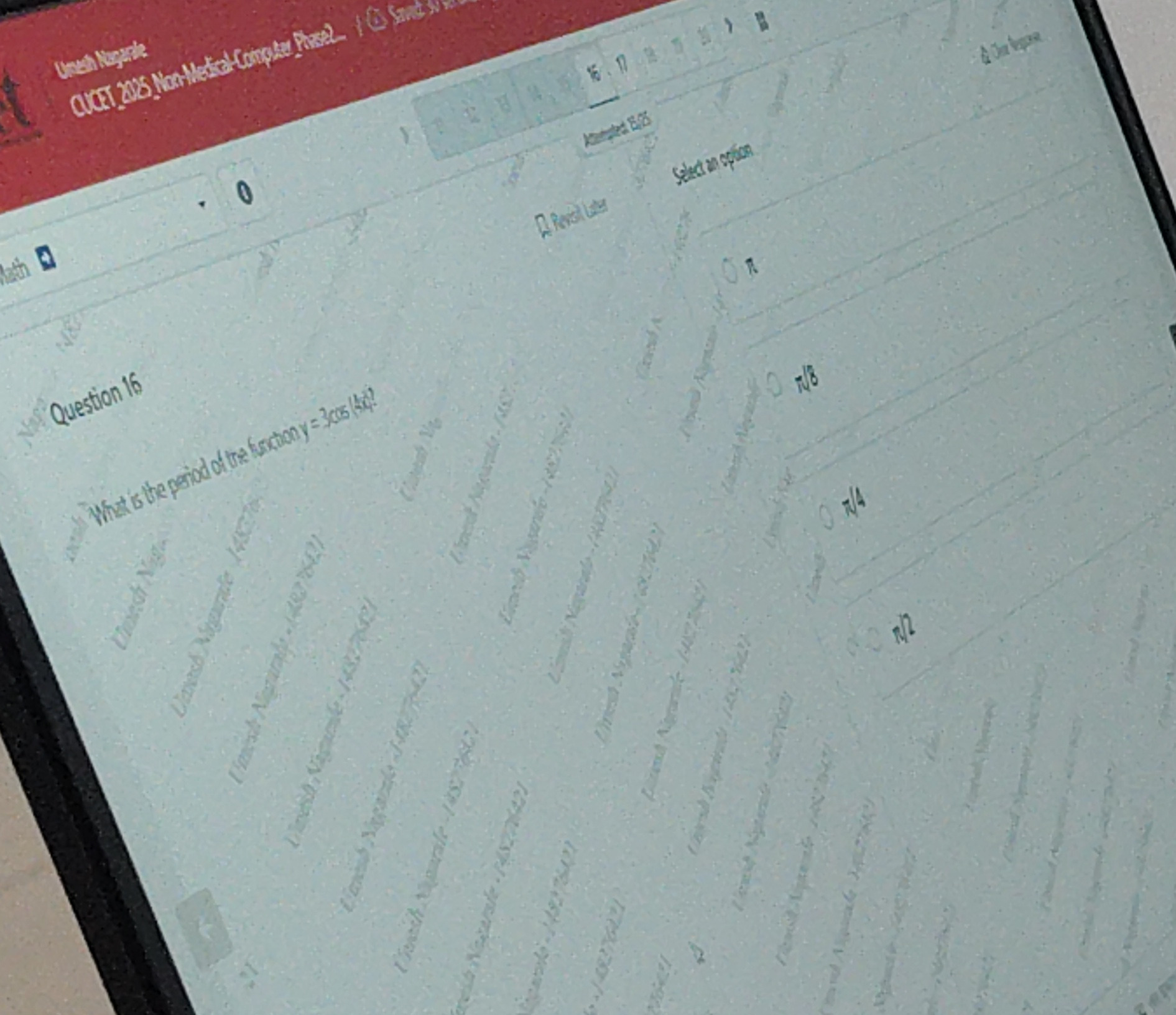
What is the period of the function y = 3cos (4t)?

• A. $\pi$
• B. $\pi/8$
• C. $\pi/4$
• D. $\pi/2$

Answer 1

Answer: (D)

$\pi/2$

Answer 2

The period of a trigonometric function of the form $y = A\cos(Bx + C) + D$ or $y = A\sin(Bx + C) + D$ is given by the formula:

$T = \frac{2\pi}{|B|}$

In the given function, $y = 3\cos(4t)$, comparing this with the general form, we have $B = 4$.

Now, substitute the value of $B$ into the period formula:

$T = \frac{2\pi}{|4|} = \frac{2\pi}{4} = \frac{\pi}{2}$

Thus, the period of the function $y = 3\cos(4t)$ is $\frac{\pi}{2}$.