Question

In a binomial distribution, if the variance is 4.5 and the number of trials is 15, what is the probability of success?

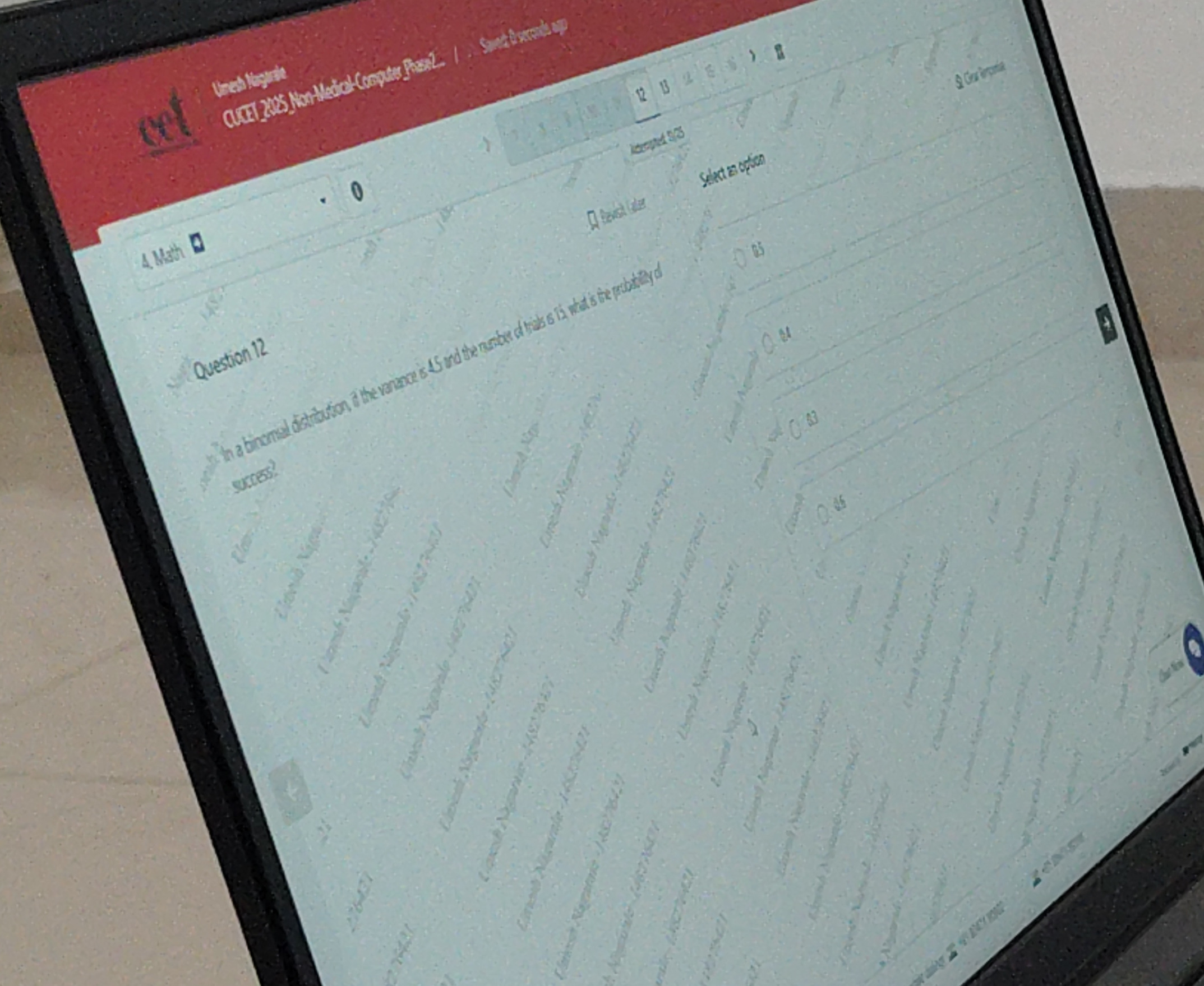
• A. 0.5
• B. 0.4
• C. 0.3

Answer 1

Answer: (A)

0.5

Answer 2

The variance of a binomial distribution is given by $\sigma^2 = np(1-p)$. Given $\sigma^2 = 4.5$ and $n=15$, we set up the equation $4.5 = 15p(1-p)$. This simplifies to $p^2 - p + 0.3 = 0$. Calculating the discriminant $D = (-1)^2 - 4(1)(0.3) = 1 - 1.2 = -0.2$. Since the discriminant is negative, there are no real solutions for $p$. This implies that a binomial distribution with $n=15$ cannot have a variance of 4.5.

The maximum possible variance for $n=15$ occurs at $p=0.5$, and its value is $15 \times 0.5 \times 0.5 = 3.75$. Given the options, and the mathematical impossibility of the stated variance, $p=0.5$ is the most plausible intended answer, assuming the question implicitly refers to the maximum variance case or has a typo in the variance value.