Question
Question: What is the range of the function $g(x) = sec(x)$?...
What is the range of the function g(x)=sec(x)?
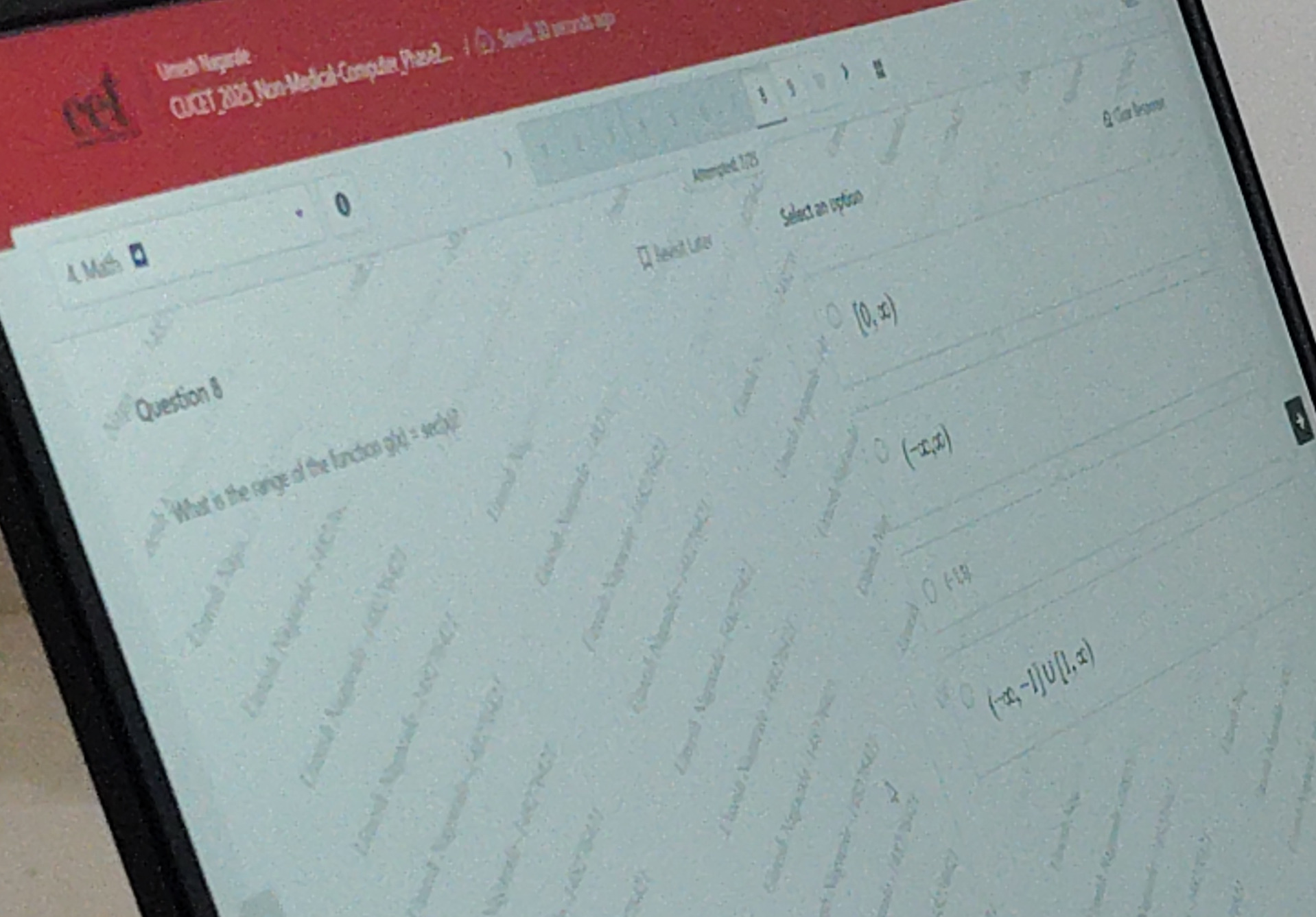
(0, ∞)
(-∞,∞)
(-1,1)
(-∞,-1]∪[1,∞)
(-∞, -1] ∪ [1, ∞)
Solution
The range of a function refers to the set of all possible output values (y-values) that the function can produce.
The given function is g(x)=sec(x). We know that sec(x) is defined as cos(x)1.
The range of the cosine function, cos(x), is [−1,1]. This means that for any real number x, −1≤cos(x)≤1.
Now, let's consider the values of sec(x)=cos(x)1 based on the values of cos(x):
-
When cos(x) is positive: If 0<cos(x)≤1: As cos(x) approaches 0 from the positive side, cos(x)1 approaches +∞. When cos(x)=1, cos(x)1=11=1. So, for 0<cos(x)≤1, the values of sec(x) are in the interval [1,∞).
-
When cos(x) is negative: If −1≤cos(x)<0: As cos(x) approaches 0 from the negative side, cos(x)1 approaches −∞. When cos(x)=−1, cos(x)1=−11=−1. So, for −1≤cos(x)<0, the values of sec(x) are in the interval (−∞,−1].
Combining these two cases, the range of sec(x) includes all real numbers except those strictly between -1 and 1. Therefore, the range of g(x)=sec(x) is (−∞,−1]∪[1,∞).
