Question

U1000.0 Figure shows two blocks connected by a light inextensible string as shown in figure. A force of $10N$ is applied on the bigger block at ${60^ \circ }$ with horizontal, then the tension in the string connecting the two masses is $10N{60^ \circ }2Kg3Kg\left( 1 \right)5N\left( 3 \right)1NSmoothsurface\left( 2 \r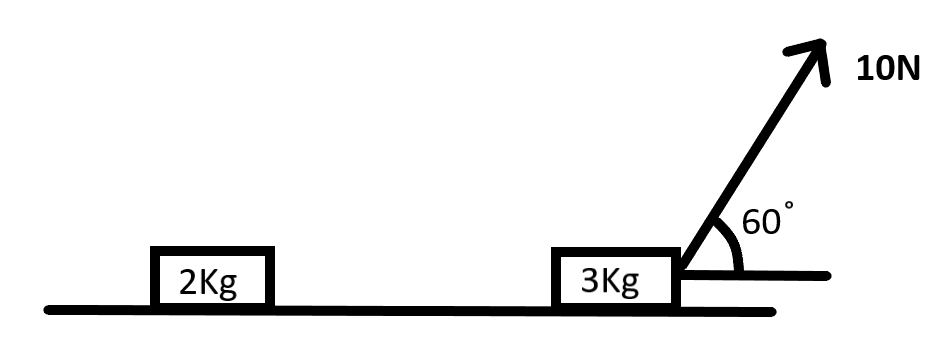ight)2N\left( 4 \right)3N$ .
\left( A \right)5N \\\ \left( B \right)1N \\\ \left( C \right)2N \\\ \left( D \right)3N \\\

Answer 1

Hint : In order to solve this question, we are first going to see what all forces are acting on the two masses and in what directions , then for the both masses, the horizontal force being present due to the $10N$ force, the acceleration is calculated for both, then by drawing the free body diagram for mass $2Kg$ , tension is calculated.
Horizontal component of force is calculated as
${F_H} = F\cos \theta$
$F = m \times a$

Complete Step By Step Answer:
As it is given that the masses are lying on a smooth surface and are connected by an inextensible string so, the only forces that are acting on the two masses are the tension in the string and the external force that is equal to $10N$ .

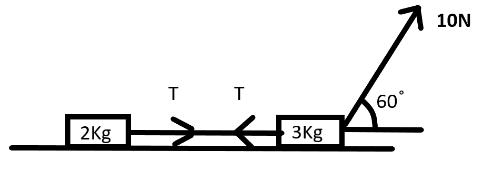
Now as we can see
$F' = 10N \times \cos {60^ \circ } = 10N \times \dfrac{1}{2} = 5N$
The acceleration of the two masses due to the horizontal component of force is
$a = \dfrac{{F'}}{{2 + 3}} = \dfrac{5}{5} = 1m{s^{ - 2}}$
If we draw the free body diagram of the mass $2Kg$ ,

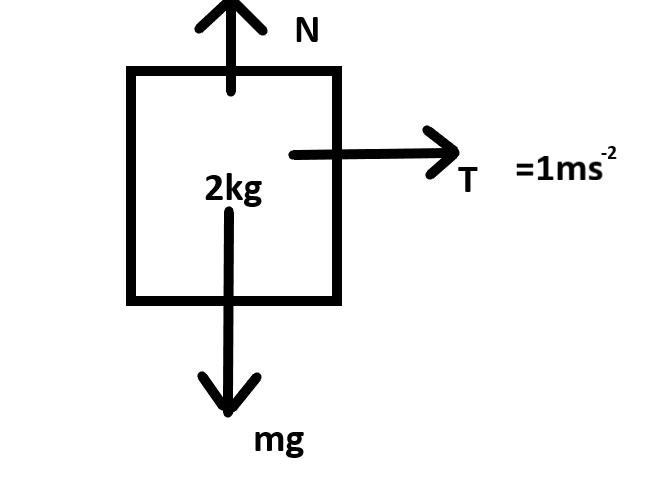
As the normal force $N$ and the weight $mg$ are balanced by each other, so, the force on this mass due to the external force is equal to tension only
$T = m \times a = 2Kg \times 1m{s^{ - 2}} = 2N$
Hence, option $\left( C \right)2N$ is the correct answer.

Note :
The acceleration is the same for both the masses due to the external force, however the components of force actually acting on the two masses is different, and that for the smaller mass is less. But the tension in the string is however just the same if we calculate by drawing the free body diagram for mass $3Kg$ .