Question

$u=0$

$g=10m/s^2$

$u=90m/s$

Find distance in 6 sec.

(ii) distance in 8 sec.

(iii) find time when $h=10m$

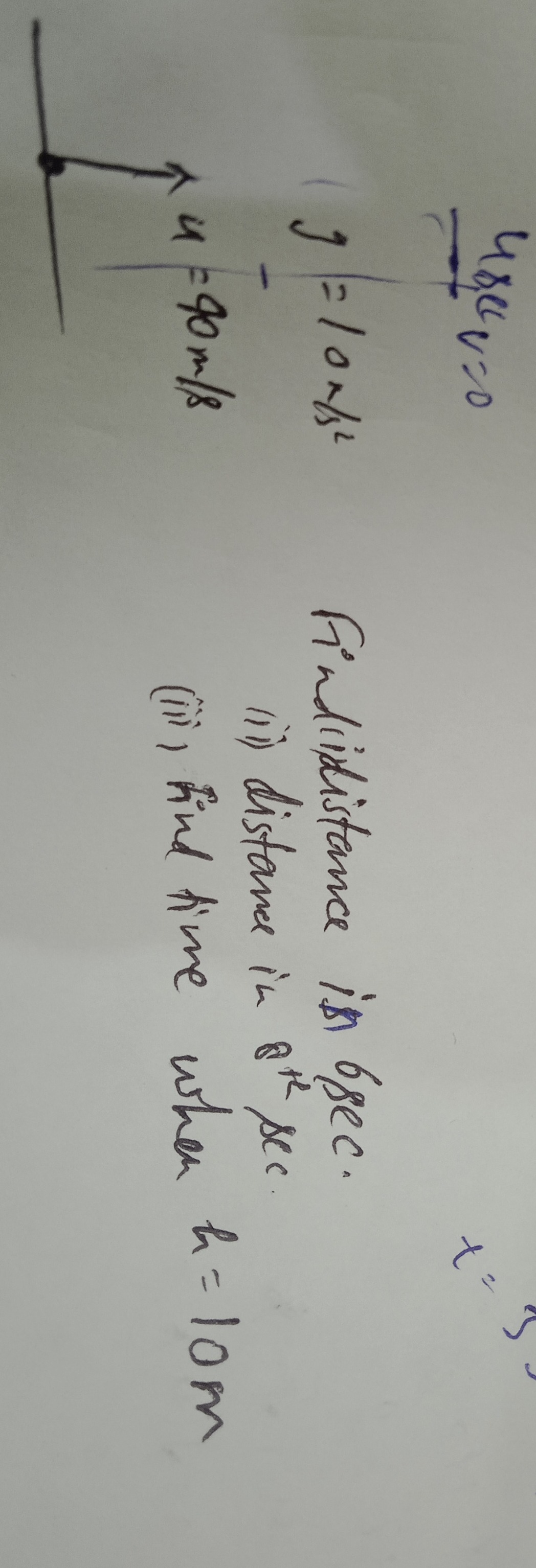
Answer 1

Distance in 6 sec = 360 m

Distance in 8 sec = 400 m

Time when $h=10\,\text{m}$:   $t = 9-\sqrt{79}$ seconds (approximately 0.11 sec) and   $t = 9+\sqrt{79}$ seconds (approximately 17.89 sec)

Answer 2

Solution:

We use the equation for vertical displacement:

$$s = ut - \tfrac{1}{2}gt^2,$$

with $u=90\,\text{m/s}$ and $g=10\,\text{m/s}^2$.

(i) Distance in 6 sec:

$$s_6=90(6)-\tfrac{1}{2}\times10\times6^2 =540-180=360\,\text{m}.$$

(ii) Distance in 8 sec:

$$s_8=90(8)-\tfrac{1}{2}\times10\times8^2 =720-320=400\,\text{m}.$$

(iii) Time when $h=10\,\text{m}$:

Set

$$90t-\tfrac{1}{2}\times10\,t^2=10 \quad \Longrightarrow \quad 90t-5t^2-10=0.$$

Rearrange:

$$5t^2-90t+10=0.$$

Divide by 5:

$$t^2-18t+2=0.$$

Solve by the quadratic formula:

$$t=\frac{18\pm\sqrt{18^2-4\times1\times2}}{2}=\frac{18\pm\sqrt{324-8}}{2}=\frac{18\pm\sqrt{316}}{2}.$$

Notice that $\sqrt{316}=2\sqrt{79}$. Thus,

$$t=\frac{18\pm2\sqrt{79}}{2}=9\pm \sqrt{79}.$$

So the two times are:

$$t=9-\sqrt{79}\quad (\approx0.11\,\text{s})\quad \text{and}\quad t=9+\sqrt{79}\quad (\approx17.89\,\text{s}).$$