Question

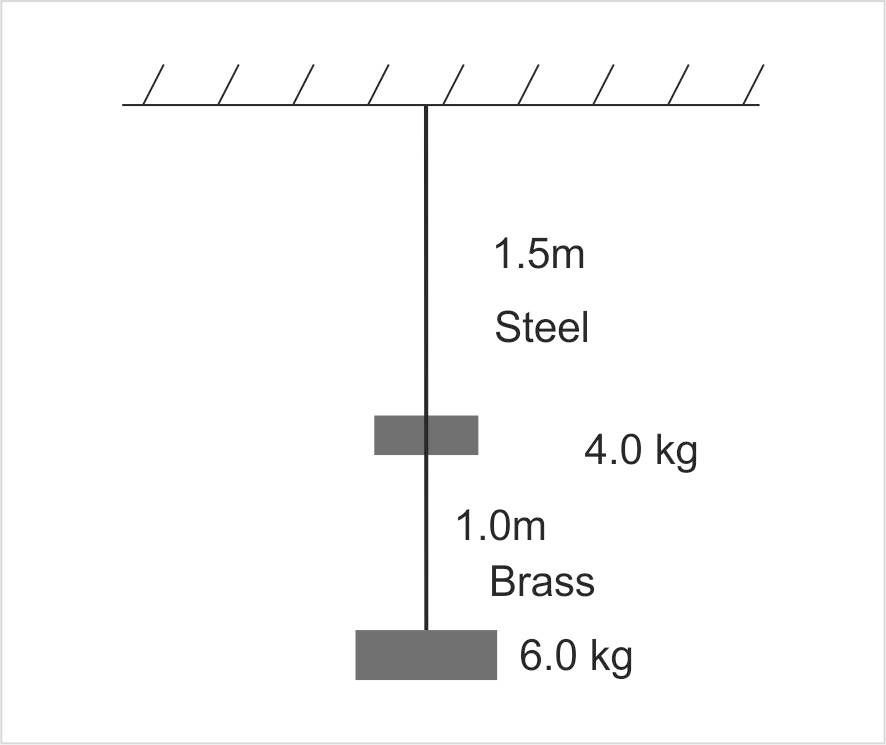
Two wires of diameter $0.25\;{\text{cm}}$, one made of steel and the other made of brass are loaded as shown in fig. $\left( 1 \right)$. The unloaded length of the steel wire is $1.5\;{\text{m}}$ and that of brass wire is $1.0\;{\text{m}}$. Compute the elongations of the steel and the brass wire. $1.5\;{\text{m}}$ Steel $4.0\;{\text{kg}}$ young’s $1.0\;{\text{m}}$ brass $6.0\;{\text{kg}}$ young’s.

Answer 1

In this question, calculate the force exerted on steel wire and the brass wire. As we know that the force is the product of the mass and acceleration due to the gravity. And also calculate the length of the steel and brass wire.

Complete step by step answer:
Consider the given figure, we have given two wires of diameter $0.25\;{\text{cm}}$, the unloaded length of the steel wire is $1.5\;{\text{m}}$ and that the unloaded length of brass wire is $1.0\;{\text{m}}$.
Let us represent the diameter by $d$ and represent the radius by $r$,
We have given the diameter of the wire is $d = 0.25\;{\text{m}}$, so radius of wire is,
$r = \dfrac{{0.25\;{\text{cm}}}}{2}$
We solve the above expression for $r$ as,
$\Rightarrow r = 0.125\;{\text{cm}}$
The length of the steel wire is, let we represent the length of the steel wire by ${L_1}$.
$\Rightarrow {L_1} = 1.5\;{\text{m}}$
The length of brass wire is, let the length of brass wire represented by ${L_2}$.
$\Rightarrow {L_2} = 1.0\;{\text{m}}$
Let us represent the force on steel wire by ${F_1}$. The expression for the force exerted on steel wire is,
$\Rightarrow F = ma$
Now, we substitute the values
$\Rightarrow {F_1} = \left( {4 + 6} \right).g$
Now we substitute the values of the acceleration due to gravity in the above equation as,
$\Rightarrow {F_1} = 10 \times 9.8$
We solve the above expression.
$\Rightarrow {F_1} = 98\;{\text{N}}$
As we know that the young’s modulus of the wire is the measure of the ability to the changes in the length of the wire. Its SI unit is Pascal. Now, the young’s modulus for steel,
$\Rightarrow {Y_1} = \dfrac{{\left( {\dfrac{{{F_1}}}{{{A_1}}}} \right)}}{{\left( {\dfrac{{\Delta {L_1}}}{{{L_1}}}} \right)}}$

Where, $\Delta {L_1}$ is the change in the length of the steel wire and ${A_1}$ is the area of cross section of the steel wire.

Now, represent the young’s modulus for steel wire by ${Y_1}$.Young’s modulus,
$\Rightarrow {Y_1} = 2.0 \times {10^{11}}\;{\text{Pa}}$
Now we substitute the values for change in length of steel wire,
$\Rightarrow \Delta {L_1} = \dfrac{{{F_1} \times {L_1}}}{{{A_1} \times {Y_1}}}$
Now we substitute the values in the above expression.
$\Rightarrow \Delta {L_1} = \dfrac{{\left( {98 \times 1.5} \right)}}{{\left[ {\pi {{\left( {0.125 \times {{10}^{ - 2}}} \right)}^2} \times 2 \times {{10}^{11}}} \right]}}$
After simplification we get,
$\Rightarrow \Delta {L_1} = 1.49 \times {10^{ - 4}}\;{\text{m}}$
Let us represent the force on steel wire by ${F_2}$. The expression for the force exerted on brass wire is,
$\Rightarrow {F_2} = \left( 6 \right)g$
Now we substitute the values in the above expression.
$\Rightarrow {F_2} = 6 \times 9.8$
Now, solve the above expression as,
$\Rightarrow {F_2} = 58.8\;{\text{N}}$
Now, represent the young’s modulus for steel wire by ${Y_2}$. The young’s modulus for brass is,
$\Rightarrow {Y_2} = \dfrac{{\left( {\dfrac{{{F_1}}}{{{A_1}}}} \right)}}{{\left( {\dfrac{{\Delta {L_1}}}{{{L_1}}}} \right)}}$

Where, $\Delta {L_2}$ is the change in the length of the steel wire and ${A_2}$ is the area of the cross section of the steel wire.
Now, Young’s modulus,
$\Rightarrow {Y_2} = 0.91 \times {10^{11}}\;{\text{Pa}}$

Now, substitute the values for change in length of steel wire,
$\Rightarrow \Delta {L_2} = \dfrac{{{F_2} \times {L_2}}}{{{A_2} \times {Y_2}}}$
Now, substitute the values in the above expression.
$\Rightarrow \Delta {L_2} = \dfrac{{\left( {58.8 \times 1} \right)}}{{\left[ {\pi {{\left( {0.125 \times {{10}^{ - 2}}} \right)}^2} \times \left( {0.91 \times {{10}^{11}}} \right)} \right]}}$
Now, solve the above expression.
$\therefore \Delta {L_2} = 1.3 \times {10^{ - 4}}\;{\text{m}}$

Therefore, the elongation of steel wire is $1.49 \times {10^{ - 4}}\;{\text{m}}$ and the elongation of brass wire is $1.3 \times {10^{ - 4}}\;{\text{m}}$.

Note: As we know that the elongation depends on the material of the wire if the cross-section and the lengths of the wires are the same. It depends on the property of the material that is the Young’s modulus.