Question

Two wires each of radius of cross section but of different materials are connected together end to end (in series). If the densities of the charge carriers in the two wires are in the ratio 1:4, the drift velocity of electrons in the two wires will be in the ratio:
a) 1:2
b) 2:1
c) 1:4
d) 4:1

Answer 1

To obtain the ratio of the drift velocity of electrons of the two materials we have to compare them using their respective equation of current expressed in terms of drift velocity. It is mentioned that the two wires are connected in series. Hence the current through both of the wires will be the same. Hence we will be able to obtain the ratio we want.

Complete step by step answer:
Let us first express current in terms of drift velocity. For that let us consider a conductor of area of cross section equal to A of diameter equal to r, carrier charge density be n and length of the conductor be d, as shown in the figure below.

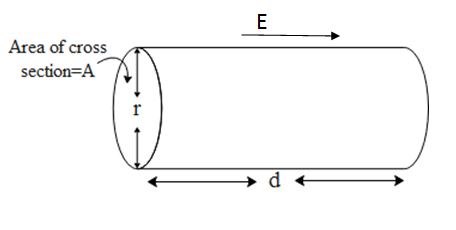
The current through the reference area is I. Let us say for an electron drift i.e. (moving with a constant drift velocity) opposite to the direction of the applied electric field. Let us say it takes time to traverse the distance d. Therefore the amount of charge that passes through the area of cross section A in time t is given by $\text{ }\\!\\!\Delta\\!\\!\text{ q=neAd}....\text{(1)}$. We know that current is defined as rate of flow of charge. Hence dividing equation 1 by t will get the current through the conductor i.e., $I=\dfrac{\text{ }\\!\\!\Delta\\!\\!\text{ q}}{t}\text{=}\dfrac{\text{neAd}}{t}$ the term$\dfrac{d}{t}\text{=}{{\text{V}}_{D}}\text{, is the value of drift velocity}$, hence substituting in the above equation the expression of I becomes $I=\text{neA}{{\text{V}}_{D}}$.
Using the above equation let us write the value of current in both the conductors.

The value of current in conductor 1 is given by ${{I}_{1}}={{\text{n}}_{1}}\text{ eA}{{\text{V}}_{\text{D}1}}...(2)$ where ${{n}_{1}}$ is the charge carrier density of conductor 1 and ${{\text{V}}_{\text{D}1}}$is the value of drift velocity of electrons in conductor 1.

The value of current in conductor 2 is given by ${{I}_{2}}={{\text{n}}_{2}}\text{ eA}{{\text{V}}_{\text{D2}}}...(3)$where ${{n}_{2}}$is the charge carrier density of conductor 2 and ${{\text{V}}_{\text{D2}}}$is the value of drift velocity of electrons in conductor 2.

Now let us divide equation 2 by 3.
$\dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{{{\text{n}}_{1}}\text{ eA}{{\text{V}}_{\text{D}1}}}{{{\text{n}}_{2}}\text{ eA}{{\text{V}}_{\text{D2}}}}$ The above wires have the same area of cross section as well as the same value of current as they are connected in series. Hence we can write ${{I}_{1}}={{I}_{2}}$. Hence the above equation can be written as,
$\dfrac{1}{1}=\dfrac{{{\text{n}}_{1}}{{\text{V}}_{\text{D}1}}}{{{\text{n}}_{2}}{{\text{V}}_{\text{D2}}}}....(4)$. It is given in the question that the ratio of the carrier charge density i.e.

conductor 1 : conductor2 = 1:4, implies $\dfrac{{{\text{n}}_{1}}}{{{\text{n}}_{2}}}=\dfrac{1}{4}$, after substituting this in equation 4 we get,
$\dfrac{1}{1}=\dfrac{{{\text{V}}_{\text{D}1}}}{\text{4}{{\text{V}}_{\text{D2}}}}$ after cross multiplying the adjacent equation be written as $\dfrac{{{\text{V}}_{\text{D}1}}}{{{\text{V}}_{\text{D2}}}}=\dfrac{4}{1}$. Hence the ratio of their drift velocity is 4:1.
Hence, the correct answer is option D.

Note:
The drift velocity of the conductor is the average velocity. The electrons accelerate by the force due to electric field and decelerate due to the obstruction caused by the ions of the metal. This increase and decrease in the velocity can be taken an average of which gives us a constant velocity i.e. drift velocity.