Question

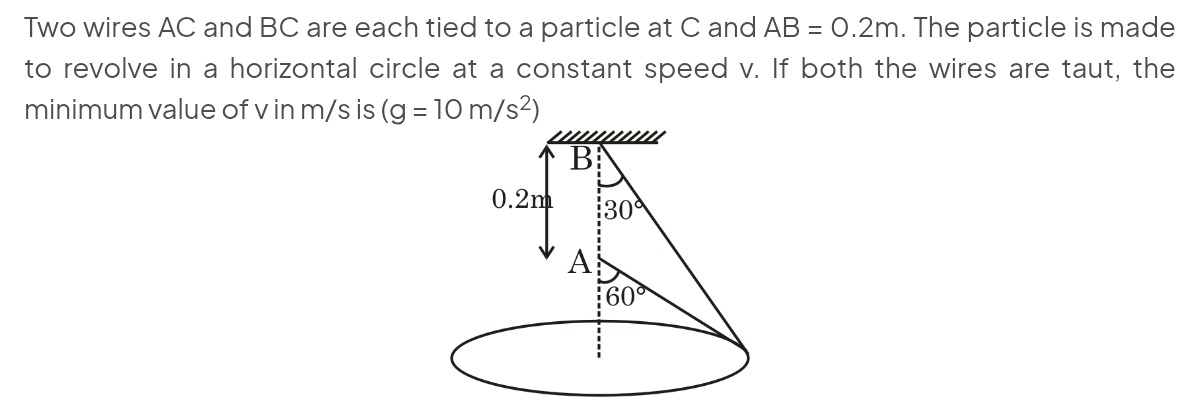
Two wires AC and BC are each tied to a particle at C and AB = 0.2m. The particle is made to revolve in a horizontal circle at a constant speed v. If both the wires are taut, the minimum value of v in m/s is (g = 10 m/s²)

• A. 0.5
• B. 1.0
• C. 1.5
• D. 2.0

Answer 1

Answer: (B)

1.0

Answer 2

1. Geometry and Radius Calculation: Let the radius of the horizontal circle be $r$. Let the vertical distance from point A to the plane of the circle be $h_A$, and from point B be $h_B$. From the given angles and the diagram: $h_A = r \cot(60^\circ) = \frac{r}{\sqrt{3}}$ $h_B = r \cot(30^\circ) = r\sqrt{3}$ Since B is 0.2m above A, the difference in their heights from the circle's plane is $h_B - h_A = 0.2$ m. Substituting the expressions for $h_A$ and $h_B$: $r\sqrt{3} - \frac{r}{\sqrt{3}} = 0.2$ $r \left(\sqrt{3} - \frac{1}{\sqrt{3}}\right) = 0.2$ $r \left(\frac{3-1}{\sqrt{3}}\right) = 0.2$ $r \left(\frac{2}{\sqrt{3}}\right) = 0.2$ $r = 0.2 \times \frac{\sqrt{3}}{2} = 0.1\sqrt{3}$ m.

2. Force Analysis: Let $T_{AC}$ and $T_{BC}$ be the tensions in wires AC and BC respectively. Let $m$ be the mass of the particle. The forces acting on the particle are:

   • Tension $T_{AC}$ making an angle $60^\circ$ with the vertical.
   • Tension $T_{BC}$ making an angle $30^\circ$ with the vertical.
   • Gravitational force $mg$ acting vertically downwards.

   For vertical equilibrium: $T_{AC} \cos(60^\circ) + T_{BC} \cos(30^\circ) = mg$ $\frac{1}{2} T_{AC} + \frac{\sqrt{3}}{2} T_{BC} = mg$ (Equation 1)

   For horizontal motion (centripetal force): $T_{AC} \sin(60^\circ) + T_{BC} \sin(30^\circ) = \frac{mv^2}{r}$ $\frac{\sqrt{3}}{2} T_{AC} + \frac{1}{2} T_{BC} = \frac{mv^2}{r}$ (Equation 2)

3. Condition for Taut Wires: For both wires to be taut, their tensions must be non-negative, i.e., $T_{AC} \ge 0$ and $T_{BC} \ge 0$. Solving Equations 1 and 2 for $T_{AC}$ and $T_{BC}$ in terms of $v$: From Equation 2, multiply by $\sqrt{3}$: $\frac{3}{2} T_{AC} + \frac{\sqrt{3}}{2} T_{BC} = \frac{\sqrt{3}mv^2}{r}$. Subtract Equation 1: $(\frac{3}{2} - \frac{1}{2}) T_{AC} = \frac{\sqrt{3}mv^2}{r} - mg \implies T_{AC} = \frac{\sqrt{3}mv^2}{r} - mg$.

   From Equation 1, multiply by $\sqrt{3}$: $\frac{\sqrt{3}}{2} T_{AC} + \frac{3}{2} T_{BC} = \sqrt{3}mg$. Subtract Equation 2: $(\frac{3}{2} - \frac{1}{2}) T_{BC} = \sqrt{3}mg - \frac{mv^2}{r} \implies T_{BC} = \sqrt{3}mg - \frac{mv^2}{r}$.

   For $T_{AC} \ge 0$: $\frac{\sqrt{3}mv^2}{r} \ge mg \implies v^2 \ge \frac{gr}{\sqrt{3}}$

   For $T_{BC} \ge 0$: $\sqrt{3}mg \ge \frac{mv^2}{r} \implies v^2 \le \sqrt{3}gr$

   Thus, for both wires to be taut, the speed $v$ must satisfy: $\frac{gr}{\sqrt{3}} \le v^2 \le \sqrt{3}gr$

4. Minimum Value of v: The minimum value of $v$ occurs at the lower bound of the inequality for $v^2$: $v_{min}^2 = \frac{gr}{\sqrt{3}}$ $v_{min} = \sqrt{\frac{gr}{\sqrt{3}}}$

5. Calculation: Substitute the values $g = 10$ m/s² and $r = 0.1\sqrt{3}$ m: $v_{min} = \sqrt{\frac{10 \times (0.1\sqrt{3})}{\sqrt{3}}}$ $v_{min} = \sqrt{\frac{1}{\sqrt{3}} \times \sqrt{3}}$ $v_{min} = \sqrt{1}$ $v_{min} = 1$ m/s.