Question
Question: Two wires A and B are carrying currents \[{{I}_{1}}\] and \[{{I}_{2}}\] as shown in the figure. The ...
Two wires A and B are carrying currents I1 and I2 as shown in the figure. The separation between them is d. A third wire Carrying a current I is kept parallel to them at a distance x from A such that net force acting on it is zero. The possible values of x are:
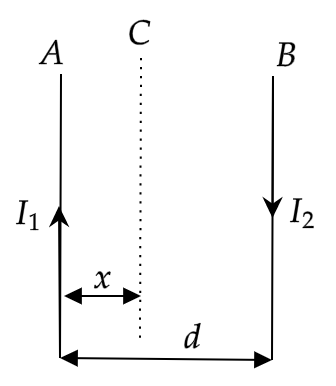
(A) x=(I1−I2I1)d and x=(I1−I2I1)d
(B) x=±(I1−I2I1)d
(C) x=(I1+I2I1)d and x=(I1−I2I2)d
(D) x=(I1+I2I2)d and x=(I1−I2I1)d
Solution
Hint In the given question, we have been provided with two current-carrying wires at a known separation and a third current-carrying wire is placed at an unknown distance somewhere between the two wires. We know that any current-carrying wire produces a magnetic field and the field thus produced will exert a force on the other current-carrying wires in its vicinity. We have been told that the force acting on the wire in the middle is zero and hence all we need to do is express the force on the wire in terms of the current and the distances between the wires and we will have our answer. Let’s see the detailed solution.
Formula Used: F=2πμ0xI′I
Complete step by step answer:
As discussed above, the force exerted on the wire C due to the wire A must be equal to the force exerted on the wire C due to the wire B.
Now we know that the force exerted on unit length of a wire carrying current I’ placed at a distance x from another wire carrying current I is given as F=2πμ0xI′I
Using this formula, we can say that
The force acting on unit length of the wire C due to wire A F1′=2πμ0xI1I
Force acting on the entire length of the wire C due to the wire A will be F1=2πμ0xI1Id
Similarly, the force acting on unit length of the wire C due to the wire B F2′=2πμ0(d−x)I2I
Now, force acting on the entire length of the wire C due to the wire B would be F2=2πμ0(d−x)I2Id
Since the net force on the wire C is zero, we can equate the two force calculated above, that is
