Question

Two wire loops A and B are placed in the X-Y plane as shown. Loop A is made out of two quarter circular sections of radii a and 2a centred at the origin and two straight sections along the X and Y axes, and has a total resistance R. Loop B is a circle of radius b centred at the origin, with b = a/100 (the sizes of the loops in the figure are not to scale). Initially both loops carry no current. A steady current I is switched on in Loop B. If the total charge that circulates in Loop A during the build-up of the current in Loop B is $(\frac{\pi}{n} \times 10^{-4})(\frac{\mu_0 a I}{R})$, then n is ______.

Answer 1

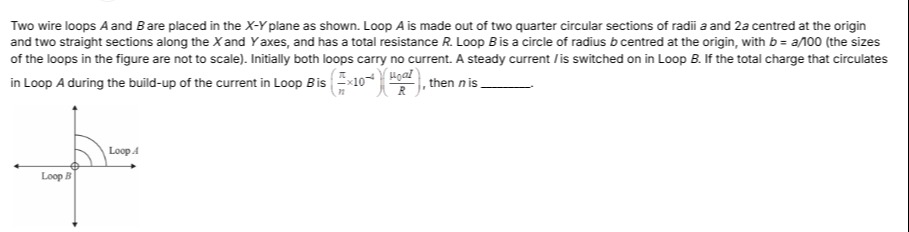
16

Answer 2

To determine the total charge circulated in Loop A, we need to calculate the change in magnetic flux through Loop A due to the current in Loop B.

1. Magnetic Field due to Loop B:

Loop B is a small circular loop of radius $b$ carrying current $I$, centered at the origin in the X-Y plane. Since $b = a/100$, $b$ is very small compared to the dimensions of Loop A ($a$ and $2a$). Therefore, Loop B can be approximated as a magnetic dipole.

The magnetic dipole moment of Loop B is $\vec{m} = I (\text{Area}) \hat{k} = I \pi b^2 \hat{k}$ (assuming the current $I$ is counter-clockwise, so the field at the center is along the positive z-axis).

The magnetic field produced by a magnetic dipole in its equatorial plane (the X-Y plane for a dipole along the Z-axis) at a distance $r$ from the origin ($r \gg b$) is given by:

$$\vec{B}(\vec{r}) = -\frac{\mu_0}{4\pi} \frac{\vec{m}}{r^3}$$

Substituting $\vec{m} = I \pi b^2 \hat{k}$:

$$\vec{B}(\vec{r}) = -\frac{\mu_0}{4\pi} \frac{I \pi b^2}{r^3} \hat{k} = -\frac{\mu_0 I b^2}{4 r^3} \hat{k}$$

This magnetic field is directed perpendicular to the X-Y plane (along the negative Z-axis).

2. Magnetic Flux through Loop A:

Loop A is a quarter-annulus in the X-Y plane, bounded by radii $a$ and $2a$ and angles from $0$ to $\pi/2$.

The magnetic flux $\Phi_A$ through Loop A is given by $\Phi_A = \int_A \vec{B} \cdot d\vec{A}$.

Since $\vec{B}$ is along the Z-axis and the area element $d\vec{A}$ for Loop A is also along the Z-axis ($d\vec{A} = dA \hat{k}$), the dot product simplifies.

In polar coordinates, $dA = r dr d\theta$.

The integral limits are $r$ from $a$ to $2a$ and $\theta$ from $0$ to $\pi/2$.

$$\Phi_A = \int_0^{\pi/2} \int_a^{2a} \left(-\frac{\mu_0 I b^2}{4 r^3}\right) r dr d\theta$$ $$\Phi_A = -\frac{\mu_0 I b^2}{4} \int_0^{\pi/2} d\theta \int_a^{2a} \frac{1}{r^2} dr$$

Evaluate the integrals:

$$\int_0^{\pi/2} d\theta = [\theta]_0^{\pi/2} = \frac{\pi}{2}$$ $$\int_a^{2a} \frac{1}{r^2} dr = \left[-\frac{1}{r}\right]_a^{2a} = -\frac{1}{2a} - \left(-\frac{1}{a}\right) = -\frac{1}{2a} + \frac{1}{a} = \frac{1}{2a}$$

Substitute these values back into the flux equation:

$$\Phi_A = -\frac{\mu_0 I b^2}{4} \left(\frac{\pi}{2}\right) \left(\frac{1}{2a}\right)$$ $$\Phi_A = -\frac{\mu_0 I b^2 \pi}{16a}$$

3. Total Charge Circulated in Loop A:

The total charge $Q$ that circulates in Loop A during the build-up of current in Loop B is given by the change in magnetic flux divided by the resistance $R$ of Loop A:

$$Q = \frac{|\Delta \Phi_A|}{R} = \frac{|\Phi_{A, \text{final}} - \Phi_{A, \text{initial}}|}{R}$$

Initially, the current in Loop B is zero, so $\Phi_{A, \text{initial}} = 0$.

Finally, the current in Loop B is $I$, so $\Phi_{A, \text{final}} = -\frac{\mu_0 I b^2 \pi}{16a}$.

Therefore, the magnitude of the change in flux is:

$$|\Delta \Phi_A| = \left|-\frac{\mu_0 I b^2 \pi}{16a} - 0\right| = \frac{\mu_0 I b^2 \pi}{16a}$$

The total charge circulated is:

$$Q = \frac{1}{R} \left(\frac{\mu_0 I b^2 \pi}{16a}\right) = \frac{\mu_0 I b^2 \pi}{16aR}$$

4. Substitute the value of b and find n:

Given $b = a/100$. Substitute this into the expression for $Q$:

$$Q = \frac{\mu_0 I (a/100)^2 \pi}{16aR} = \frac{\mu_0 I (a^2/10000) \pi}{16aR}$$ $$Q = \frac{\mu_0 I a^2 \pi}{16 \times 10000 \times a R} = \frac{\mu_0 I a \pi}{160000 R}$$

To match the given form $(\frac{\pi}{n} \times 10^{-4})(\frac{\mu_0 a I}{R})$, we can rewrite $Q$ as:

$$Q = \frac{\pi}{16 \times 10^4} \frac{\mu_0 a I}{R} = \left(\frac{\pi}{16} \times 10^{-4}\right) \left(\frac{\mu_0 a I}{R}\right)$$

Comparing this with the given expression, we find:

$$\frac{\pi}{n} = \frac{\pi}{16}$$

Thus, $n = 16$.