Solveeit Logo
Login

Question

Question: Two wheels \(1\) and \(2\) of radii \({r_1}\) and \({r_2}\) are connected by a belt. If the belt doe...

Two wheels 11 and 22 of radii r1{r_1} and r2{r_2} are connected by a belt. If the belt does not slip on the wheels and angular speed of wheel 11 is ω\omega then acceleration of P relative to Q is

A. r1ω2(1+r2r1){r_1}{\omega ^2}(1 + \dfrac{{{r_2}}}{{{r_1}}})
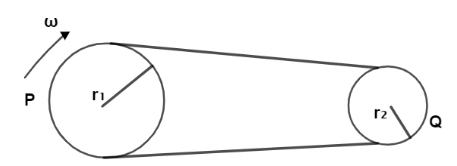
B. r1ω2(1+r1r2){r_1}{\omega ^2}(1 + \dfrac{{{r_1}}}{{{r_2}}})
C. r1ω2{r_1}{\omega ^2}
D. r1ω2(1+r2r22){r_1}{\omega ^2}(1 + \dfrac{{{r_2}}}{{{r_2}^2}})

Explanation

Solution

In order to solve this problem we need to understand angular acceleration which states that angular acceleration is the time derivative of angular velocity whereas angular velocity is the time derivation of angle which body rotates in some period.On a moving body around the axis each particle has its velocity along the tangent and it is equal to the product of angular velocity and radius in which it is moving.

Complete step by step answer:
Here we use formulas of angular velocity and angular acceleration.
Let ω\omega be angular velocity and “v” be its speed.
Then from relation v=rωv = r\omega for the first wheel is v=r1ωv = {r_1}\omega .
And for second let it rotates with angular velocity ω2{\omega _2} so using relation of speed we get
v=r2ω2v = {r_2}{\omega _2}
Equating both speed we get r1ω=r2ω2{r_1}\omega = {r_2}{\omega _2}
⇒ω2=r1ωr2\Rightarrow {\omega _2} = \dfrac{{{r_1}\omega }}{{{r_2}}}
We know from relativity that α⃗PQ=α⃗P−α⃗Q{\vec \alpha _{PQ}} = {\vec \alpha _P} - {\vec \alpha _Q}
Where α\alpha is angular acceleration

Also using α=rω2\alpha = r{\omega ^2}
We get α⃗p=r1ω2i^{\vec \alpha _p} = {r_1}{\omega ^2}\hat i and α⃗Q=−r2ω22i^{\vec \alpha _Q} = - {r_2}{\omega _2}^2\hat i
Using value of ω2{\omega _2} we get α⃗Q=r2(r12ω2r22)i^{\vec \alpha _Q} = {r_2}(\dfrac{{{r_1}^2{\omega ^2}}}{{{r_2}^2}})\hat i
⇒α⃗Q=−r12ω2r2i^\Rightarrow {\vec \alpha _Q} = - \dfrac{{{r_1}^2{\omega ^2}}}{{{r_2}}}\hat i
⇒α⃗PQ=r1ω2i^+r12ω2r2i^\Rightarrow {\vec \alpha _{PQ}} = {r_1}{\omega ^2}\hat i + \dfrac{{{r_1}^2{\omega ^2}}}{{{r_2}}}\hat i
∴α⃗PQ=r1ω2[1+r1r2]i^\therefore {\vec \alpha _{PQ}} = {r_1}{\omega ^2}\left[ {1 + \dfrac{{{r_1}}}{{{r_2}}}} \right]\hat i

So the correct option is B.

Note: It should be remembered that the direction of angular acceleration of Q is opposite to that of P because due to belt wrapping Q the wheel moves in the opposite direction so that belt is stationary. If both moves in the same direction then the belt starts moving due to the same directional force applied on it and hence our calculation goes wrong. Also when second wheel motion is analyzed with respect to first the second wheel is assumed to be at rest.