Question

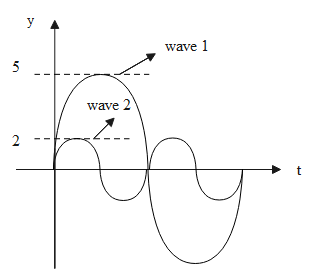
Two waves in the same medium are represented by y-t curves in the figure. Find the ratio of their average intensities?

Answer 1

The intensity of the wave is directly proportional to the angular frequency and the amplitude. The angular frequency is the product of 2(pi) times the frequency. The frequency is inversely proportional to the wavelength of the wave. Thus, the ratio of intensities is computed as the ratio of the product of wavelength and the amplitude of the waves.
Formula used:
$I\propto \omega A$

Complete answer:
From the given information, we have the data as follows.
The amplitude of the wave 1 is, 5 and the amplitude of the wave 2 is 2.
The wavelength of wave 1 is, 1 m and the wavelength of wave 2 is 2 m.
The relation between the intensity, the amplitude and the wavelength of the wave is given as follows.
$I\propto \omega A$
The ratio of the intensities is given as follows.
$\dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{\omega _{1}^{2}\times A_{1}^{2}}{\omega _{2}^{2}\times A_{2}^{2}}$
Represent the angular frequency in terms of the frequency.

& \dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{2\pi f_{1}^{2}\times A_{1}^{2}}{2\pi f_{2}^{2}\times A_{2}^{2}} \\\ & \therefore \dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{f_{1}^{2}\times A_{1}^{2}}{f_{2}^{2}\times A_{2}^{2}} \\\ \end{aligned}$$ The relation between the frequency, the velocity and the wavelength of the wave is given as follows. $$\begin{aligned} & v=f\lambda \\\ & \Rightarrow f\propto \dfrac{1}{\lambda } \\\ & \therefore \dfrac{{{f}_{1}}}{{{f}_{2}}}=\dfrac{{{\lambda }_{2}}}{{{\lambda }_{1}}} \\\ \end{aligned}$$ Now substitute this relation between the frequency and the wavelength of the waves. $$\dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{\lambda _{2}^{2}\times A_{1}^{2}}{\lambda _{1}^{2}\times A_{2}^{2}}$$ As we know the values of the amplitude and the wavelength of the waves, so, substitute the same in the above equation. $$\dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{{{1}^{2}}\times {{5}^{2}}}{{{2}^{2}}\times {{2}^{2}}}$$ Continue further computation. $$\begin{aligned} & \dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{1\times 25}{4\times 4} \\\ & \therefore \dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{25}{16} \\\ \end{aligned}$$ $$\therefore $$ The ratio of the average intensities of the waves in the same medium is 25 : 16. **Note:** The frequency is inversely proportional to the wavelength of the wave. We have derived the values of the wavelength of the waves using the y-t graph. The wavelength equals the distance between the successive crests or the troughs. The crest is a point on the wave with a maximum value of the amplitude or with the maximum displacement value and the trough is a point on the wave with a minimum value of the amplitude or with the minimum displacement value.