Solveeit Logo
Login

Question

Question: Two vessels \(A\) and \(B\) of different shapes have the same base area and are filled with water up...

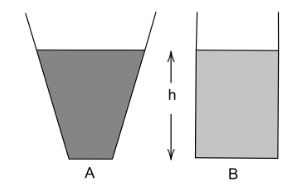
Two vessels AA and BB of different shapes have the same base area and are filled with water up to the same height hh (see figure). The force exerted by water on the base is FAF_A for vessel AA and FBF_B for vessel BB. The respective weights of the water filled in vessels are WAW_A and WBW_B, Then
A. FA>FB;WA>WB{F_A} > {F_B};{W_A} > {W_B}
B. FA=FB;WA>WB{F_A} = {F_B};{W_A} > {W_B}
C. FA=FB;WA<WB{F_A} = {F_B};{W_A} < {W_B}
D. FA>FB;WA=WB{F_A} > {F_B};{W_A} = {W_B}

Explanation

Solution

We will start by analyzing the notes given within the question. It is given that the area of both the vessels is the same. The pressure is additionally an equivalent because the vessels are of an equivalent height. Since, area and pressure are an equivalent for both the vessels, the connection between the force on each can be found out . This provides us half the answer to the question. The second part of the question concerns the load of the liquid in both of the vessels.

Complete step by step answer:
It is given that the area of both the vessels is the same. The pressure is additionally an equivalent because the vessels are of an equivalent height. Since area and pressure are an equivalent for both the vessels, if pressure and area are an equivalent , then force must be an equivalent also because P=FAP = \dfrac{F}{A}. Thus, FA=FB{F_A} = {F_B}

The liquid exerts pressure (this pressure is named fluid pressure or hydrostatic pressure), and hence force, not only on the bottom but also on the edges of the vessel. This force is normal to the edges of the vessel. For vessel B, this force has no component within the downward direction. Within the case of vessel A, this force features a non-zero component vertically downwards. Hence vessel A gives a better reading than vessel B once they are weighed on a weighing scale.Thus, WA>WB{W_A} > {W_B}

Therefore, the correct answer is option B.

Note: The particles of fluids are constantly moving in all directions at random. As the particles move they keep bumping into one another and into anything in their path. These collisions cause pressure, and therefore the pressure is exerted equally in all directions.Pressure is proportional to both depth and weight density.