Question

Two very long, straight and insulated wires are kept at ${90^0}$ angle from each other in an xy plane as shown in the figure. These wires carry currents of equal magnitude I, whose directions are shown in the figure. The net magnetic field at point P will be :

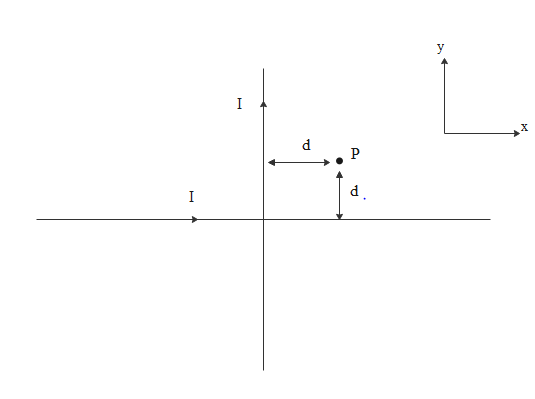
A. Zero
B. $\dfrac{{ + {\mu _0}I}}{{\pi d}}\left( {\mathop Z\limits^ \wedge } \right)$
C. $\dfrac{{ - {\mu _0}I}}{{2\pi d}}\left( {\mathop X\limits^ \wedge + \mathop Y\limits^ \wedge } \right)$
D. $\dfrac{{ + {\mu _0}I}}{{2\pi d}}\left( {\mathop X\limits^ \wedge + \mathop Y\limits^ \wedge } \right)$

Answer 1

When charge is at rest it produces only electric fields but when charge is under motion it produces both electric and magnetic fields. A current carrying conductor produces a magnetic field. Here the magnetic field produced by straight long wire will be found by ampere circuital law.
Formula used:
$B = \dfrac{{{\mu _0}I}}{{2\pi d}}\mathop n\limits^ \wedge$

Complete answer:
Electricity and magnetism are interdependent on each other. Motion of the magnet in the conducting loop generates the eddy currents while motion of charge in the conductor produces the magnetic field around it.
In case of current carrying a long conductor we will consider an circular ampere loop which will be in a plane perpendicular to the current carrying direction. On any point of the loop the magnitude of the magnetic field will be the same.
That magnetic field is given by
$B = \dfrac{{{\mu _0}I}}{{2\pi d}}\mathop n\limits^ \wedge$
Where ‘I’ is the current carrying in conductor and ‘d’ is the perpendicular distance between conductor and the point where magnetic field need to be found and $\mathop n\limits^ \wedge$ is the direction of normal to the plane containing current carrying wire and the point where we should find the magnetic field.
By referring to the diagram below we can understand the given situation.

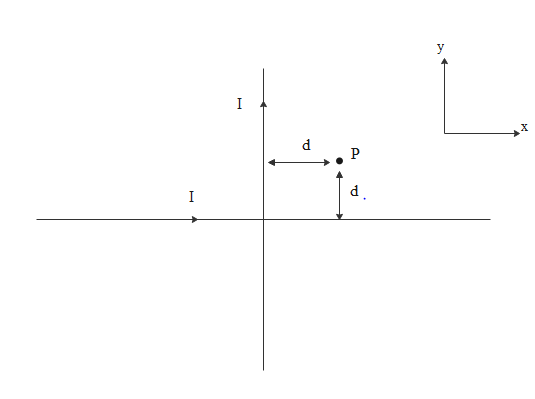
To find the direction of the magnetic field at a point due to a wire, place the right hand thumb along the current carrying direction and curl the right hand fist along the point where the magnetic field needs to be found.
So magnetic field due to vertical wire will be into the plane i.e along the negative z axis and due to horizontal wire will be out of the plane i.e along positive z axis. Magnitude of magnetic fields in both cases will be $B = \dfrac{{{\mu _0}I}}{{2\pi d}}$
So magnetic fields are the same in magnitude and opposite in direction. So the net magnetic field will be zero.

Hence option A will be answered.

Note:
From the given question, if we change the direction of any of one current then the resultant magnetic field will not be zero. They will add up. Magnitude will be the same in both cases, but the direction will be varying. We can find the direction of the magnetic field anywhere by drawing the ampere loop over there.