Question
Question: Two very long line charges of uniform linear charge density \( + \lambda \) and \( - \lambda \) are ...
Two very long line charges of uniform linear charge density +λ and −λ are placed along the same line with the separation between the nearest ends being 2a, as shown in the figure. The electric field intensity at a point O is:
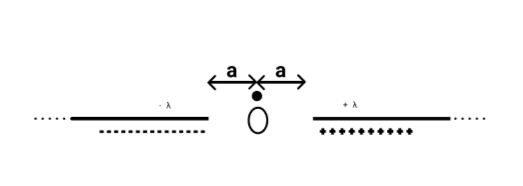
(a) 0
(b) πε0aλ
(c) 2πε0aλ
(d) 4πε0aλ
Solution
In this inquiry, we need to locate the electric field force at the point O. So by using the formula for the force on the charged particle due to the section given there. Both will have the same amount of force. The formula will be dF=kQλdx/x2. So by using this we will calculate the force.
Formula used:
Force on the charged particles,
dF=kQλdx/x2
Here,
dF, will be a change in the force
k, will be the Boltzmann constant
x, will be the distance
Complete step by step solution:
So here, most importantly we will ascertain the power of the charged molecule
Therefore, the force on the charged particle is given by
dF=kQλdx/x2
Now on integrating the above equation, we get
⇒F=a∫∞x2kQλdx
So, on solving the integration, we will take out the constant part and then put the limit on the rest.
We get
⇒F=kQλ[x−1]a∞
So on solving the limit, we get
⇒F=kQλa1
And it can also be written as
⇒F=akQλ
Since the negative section creates an equal amount of force in the same direction.
So the force for positive and negative will be the same.
Therefore, the total force will be equal to
⇒FTotal=akQλ+akQλ
⇒FTotal=a2kQλ
And also it can be written as
⇒FTotal=a2kλ
And as we know k=4πε01
So the above equation can also be written as
⇒FTotal=2πε0aλ
So the correct option will be C
Notes The course of the Electric line of power for a positive and negative charge. For a positive charge, the electric line moves away and for a negative charge move towards it. At the point when two inverse charges are set shut to one another, they get pulled in. The positive charge Moves toward the electric line of power and goes into a negative charge field which causes the line bend. Two same charges repulse one another.
