Question

Two vertices of the triangle are $\left( -1,4 \right)$ and $\left( 5,2 \right)$ . If the centroid is $\left( 0,-3 \right)$ , then the third vertex of the triangle is.
(a) $\left( -4,-15 \right)$
(b) $\left( 4,-15 \right)$
(c) $\left( -4,15 \right)$
(d) $\left( 2,3 \right)$

Answer 1

Hint : For solving this question first we will assume the coordinates of the third vertex of the given triangle to be at point $\left( h,k \right)$ . After that, we will apply the formula for the coordinates of the centroid of any triangle $O\equiv \left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$ where $\left( {{x}_{1}},{{y}_{1}} \right)$ $\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$ are the vertices of the triangle. Then, we will solve to get the values of $h$ and $k$ easily.

Complete step by step solution :
Given:
It is given that there is a triangle whose centroid is at point $\left( 0,-3 \right)$ and coordinates of two vertices are $\left( -1,4 \right)$ and $\left( 5,2 \right)$ . And we have to find the coordinates of the third vertex of the given triangle.
Now, let the given triangle is $\Delta ABC$ and the centroid is at the point $O$ where, $A\equiv \left( -1,4 \right)$ , $B\equiv \left( 5,2 \right)$ , $C\equiv \left( h,k \right)$ and $O\equiv \left( 0,-3 \right)$ .
Now, before we proceed we should know that if there is a $\Delta ABC$ where, $A\equiv \left( {{x}_{1}},{{y}_{1}} \right)$ , $B\equiv \left( {{x}_{2}},{{y}_{2}} \right)$ and $C\equiv \left( {{x}_{3}},{{y}_{3}} \right)$ . Then, the centroid of the $\Delta ABC$ will be at the point $O\equiv \left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$ .
Now, we will use this result for solving this question.
Now, as per our assumption $\Delta ABC$ and centroid is at the point $O$ where, $A\equiv \left( -1,4 \right)$ , $B\equiv \left( 5,2 \right)$ , $C\equiv \left( h,k \right)$ so, we have ${{x}_{1}}=-1;{{x}_{2}}=5;{{x}_{3}}=h$ and ${{y}_{1}}=4;{{y}_{2}}=2;{{y}_{3}}=k$ . Then,
$\begin{aligned} & O\equiv \left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right) \\\ & \Rightarrow O\equiv \left( \dfrac{-1+5+h}{3},\dfrac{4+2+k}{3} \right) \\\ \end{aligned}$
$\Rightarrow O\equiv \left( \dfrac{4+h}{3},\dfrac{6+k}{3} \right)$
Now, as it is given that the centroid of the $\Delta ABC$ is at the point $O\equiv \left( 0,-3 \right)$ . Then,
$\begin{aligned} & \dfrac{4+h}{3}=0 \\\ & \Rightarrow h=-4 \\\ & \dfrac{6+k}{3}=-3 \\\ & \Rightarrow k=-15 \\\ \end{aligned}$
Now, from the above result, we conclude that coordinates of the point $C$ will be (-4,-15). For better clarity look at the figure given below:

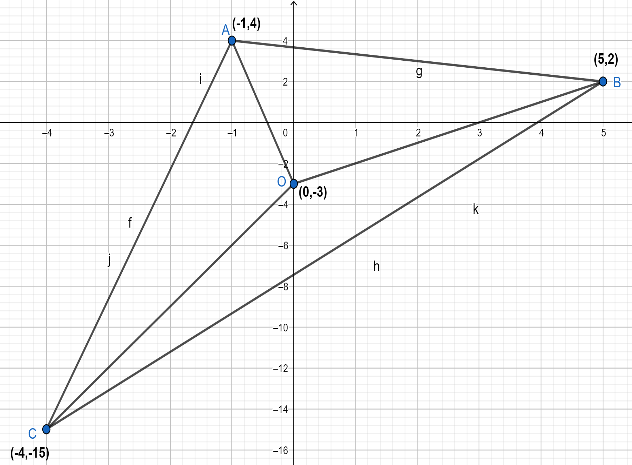
Thus, the third vertex of the given triangle will be at point $\left( -4,-15 \right)$ .
Hence, option (a) will be the correct option.

Note : Here, the student should first understand what is asked in the question and then proceed in the right direction to get the correct answer quickly. Moreover, though the problem is very easy, we should use the formula for the coordinates of the centroid of a triangle correctly and avoid calculation mistakes while solving and after getting the result we should plot the given triangle on the graph for better understanding.