Solveeit Logo
Login

Question

Question: Two vertices of a triangle are \(\left( 5,-1 \right)\) and \(\left( -2,3 \right)\). If orthocenter i...

Two vertices of a triangle are (5,−1)\left( 5,-1 \right) and (−2,3)\left( -2,3 \right). If orthocenter is the origin then coordinates of the third vertex are
1) (7,4)1)\text{ }\left( 7,4 \right)
2) (−4,7)2)\text{ }\left( -4,7 \right)
3) (4,−7)3)\text{ }\left( 4,-7 \right)
4) (−4,−7)4)\text{ }\left( -4,-7 \right)

Explanation

Solution

In this question we have been given a triangle and its two vertices with the orthocenter of the triangle being the origin. We have to find the coordinates of the third vertex. We will solve this question by finding the slope of the various lines present in the triangle and use the property that the product of the slope of parallel lines is −1-1. We will then create equations based on the values given and solve them to get the required coordinates.

Complete step by step answer:
We have the coordinates of the two vertices of the triangle as (5,−1)\left( 5,-1 \right) and (−2,3)\left( -2,3 \right), and the orthocenter being (0,0)\left( 0,0 \right). The triangle can be constructed as:

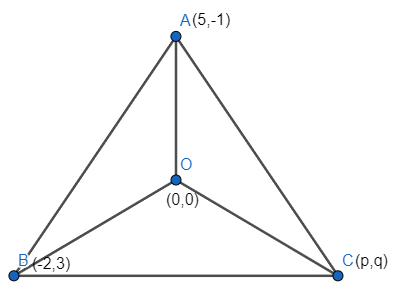
Now we know the formula for calculating the slope of a line is given by m=y2−y1x2−x1m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}
Now we have slope of AOAO as:
⇒mAO=−1−05−0\Rightarrow {{m}_{AO}}=\dfrac{-1-0}{5-0}
On simplifying, we get:
⇒mAO=−15\Rightarrow {{m}_{AO}}=-\dfrac{1}{5}
Now we have slope of BCBC as:
⇒mBC=q−3p−(−2)\Rightarrow {{m}_{BC}}=\dfrac{q-3}{p-\left( -2 \right)}
On simplifying, we get:
⇒mBC=q−3p+2\Rightarrow {{m}_{BC}}=\dfrac{q-3}{p+2}
Now since we can see that AO⊥BCAO\bot BC, we can write the product of both the slopes as −1-1. Mathematically, we get:
⇒mAO×mBC=−1\Rightarrow {{m}_{AO}}\times {{m}_{BC}}=-1
On substituting the values of the slopes, we get:
⇒−15×q−3p+2=−1\Rightarrow -\dfrac{1}{5}\times \dfrac{q-3}{p+2}=-1
On simplifying and rearranging, we get:
⇒q=5p+13→(1)\Rightarrow q=5p+13\to \left( 1 \right)
Now again we have slope of BOBO as:
⇒mBO=3−0−2−0\Rightarrow {{m}_{BO}}=\dfrac{3-0}{-2-0}
On simplifying, we get:
⇒mBO=−32\Rightarrow {{m}_{BO}}=-\dfrac{3}{2}
Now we have slope of ACAC as:
⇒mAC=q−(−1)p−5\Rightarrow {{m}_{AC}}=\dfrac{q-\left( -1 \right)}{p-5}
On simplifying, we get:
⇒mAC=q+1p−5\Rightarrow {{m}_{AC}}=\dfrac{q+1}{p-5}
Now since we can see that BO⊥ACBO\bot AC, we can write the product of both the slopes as −1-1. Mathematically, we get:
⇒mBO×mAC=−1\Rightarrow {{m}_{BO}}\times {{m}_{AC}}=-1
On substituting the values of the slopes, we get:
⇒−32×q+1p−5=−1\Rightarrow -\dfrac{3}{2}\times \dfrac{q+1}{p-5}=-1
On simplifying and rearranging, we get:
⇒q=2p−133→(2)\Rightarrow q=\dfrac{2p-13}{3}\to \left( 2 \right)
Now we have two equations which we will solve. Since the left-hand side of both the equations is the same, we can write:
⇒5p+13=2p−133\Rightarrow 5p+13=\dfrac{2p-13}{3}
On cross multiplying the terms, we get:
⇒15p+39=2p−13\Rightarrow 15p+39=2p-13
On rearranging, we get:
⇒15p−2p=−13−39\Rightarrow 15p-2p=-13-39
On simplifying, we get:
⇒13p=−52\Rightarrow 13p=-52
Therefore, we have:
⇒p=−4\Rightarrow p=-4
On substituting the value of pp in equation (1)\left( 1 \right), we get:
⇒q=5(−4)+13\Rightarrow q=5\left( -4 \right)+13
On simplifying, we get:
⇒q=−7\Rightarrow q=-7
Therefore, we have the coordinates as (p,q)=(−4,−7)\left( p,q \right)=\left( -4,-7 \right), which is the third vertex.

So, the correct answer is “Option 4”.

Note: In this question we have used the property of the product of the slope of perpendicular lines. Various properties of triangles and angles should be remembered while doing these types of questions. It is to be remembered that the orthocenter of a triangle is like the center of the triangle and the slope of the line represents the gradient of the line.