Solveeit Logo
Login

Question

Question: Two vertices of a triangle are \(\left( 1,3 \right)\) and \(\left( 4,7 \right)\) .The orthocentre li...

Two vertices of a triangle are (1,3)\left( 1,3 \right) and (4,7)\left( 4,7 \right) .The orthocentre lies on the line x+y=3x+y=3 . The locus of the third vertex is:
A. x2−2xy+2y2−3x−4y+36=0{{x}^{2}}-2xy+2{{y}^{2}}-3x-4y+36=0
B. 2x2−4xy+3y2−4x−y+42=02{{x}^{2}}-4xy+3{{y}^{2}}-4x-y+42=0
C. 3x2+xy−4y2−2x+24y−40=03{{x}^{2}}+xy-4{{y}^{2}}-2x+24y-40=0
D. x2−4xy+3y2−2x−y+40=0{{x}^{2}}-4xy+3{{y}^{2}}-2x-y+40=0

Explanation

Solution

Hint : Orthocentre is the point of intersections of perpendiculars drawn from vertex to the opposite side of the triangle.
Equation of line with slope mm and passing through (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) is given as y−y1=m(x−x1)y-{{y}_{1}}=m\left( x-{{x}_{1}} \right) .

Complete step by step solution :
Let PQRPQR be the given triangle and P=(h,k)P=\left( h,k \right) be the vertex whose locus is to be found.
In the question it is given that the co-ordinates of vertex QQ are (1,3)\left( 1,3 \right) and the co-ordinates of vertex RR are (4,7)\left( 4,7 \right) .

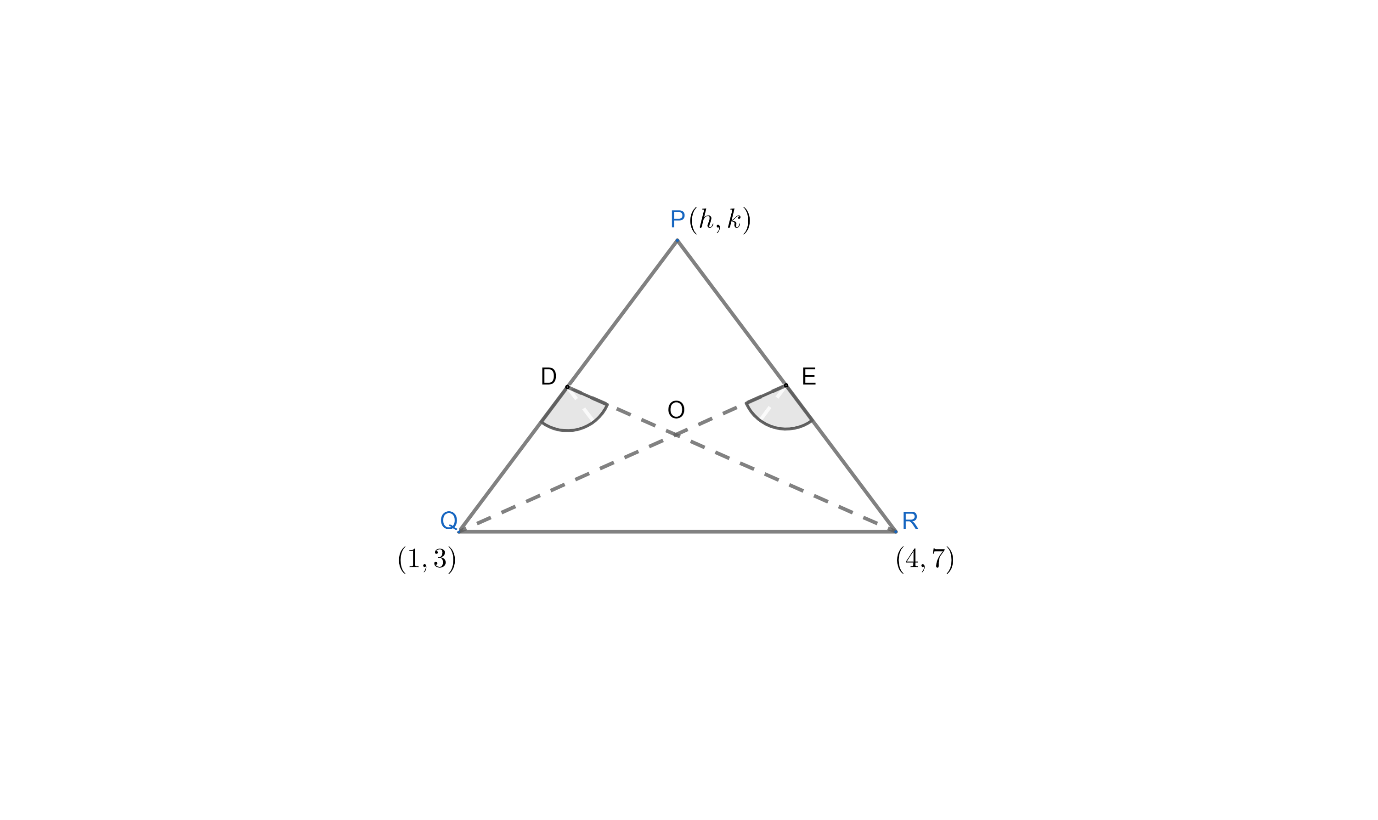
Let the coordinates of the orthocentre be (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) . Now , from the question we can conclude that (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) satisfy the equation x+y=3x+y=3 .
So, x1+y1=3{{x}_{1}}+{{y}_{1}}=3
⇒y1=3−x1\Rightarrow {{y}_{1}}=3-{{x}_{1}}
So , the coordinate of the orthocentre becomes (x1,3−x1)\left( {{x}_{1}},3-{{x}_{1}} \right) .
Now , consider the figure.
Since OO is the orthocentre , so RE⊥QERE\bot QE . Now, Q, O and E are collinear. So, the slope of line QE is equal to slope of line QO. Also, R, E and P are collinear. So, slope of RP = slope of RE. RD is perpendicular to QP. R, O and D are collinear. So, slope of RO = slope of RD. Also, Q, D and P are collinear. So, slope of QD = slope of QP.

Now , we know , the slope of the line joining two points (x1,y1)({{x}_{1}},{{y}_{1}}) and (x2,y2)({{x}_{2}},{{y}_{2}}) is given as m=y2−y1x2−x1m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}.
So, the slope of QE = slope of QO=3−x1−3x1−1=x11−x1QO=\dfrac{3-{{x}_{1}}-3}{{{x}_{1}}-1}=\dfrac{{{x}_{1}}}{1-{{x}_{1}}} and the slope of RD = slope of RO = 7−(3−x1)4−x1=4+x14−x1\dfrac{7-\left( 3-{{x}_{1}} \right)}{4-{{x}_{1}}}=\dfrac{4+{{x}_{1}}}{4-{{x}_{1}}} .
We know that if two lines are perpendicular to each other , then the product of their slopes is equal to −1-1 .
So , slope of RE ×\times slope of QE = -1
⇒\Rightarrow Slope of RE ×x11−x1=−1\times \dfrac{{{x}_{1}}}{1-{{x}_{1}}}=-1
⇒\Rightarrow Slope of RE =x1−1x1=\dfrac{{{x}_{1}}-1}{{{x}_{1}}}
Also, QD⊥RDQD\bot RD .
So, slope of QD×QD\times slope of RD=−1RD=-1
⇒\Rightarrow Slope of QD ×4+x14−x1=−1\times \dfrac{4+{{x}_{1}}}{4-{{x}_{1}}}=-1
⇒\Rightarrow Slope of QD =x1−4x1+4=\dfrac{{{x}_{1}}-4}{{{x}_{1}}+4}
Now, let’s find the equation of PE&PDPE\And PD .
We know, equation of line with slope mm and passing through (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) is given as y−y1=m(x−x1)y-{{y}_{1}}=m\left( x-{{x}_{1}} \right) .
So, equation of PEPE is given as (y−7)=x1−1x1(x−4)\left( y-7 \right)=\dfrac{{{x}_{1}}-1}{{{x}_{1}}}\left( x-4 \right) .
[We take x1{{x}_{1}} and y1{{y}_{1}} as (4,7)\left( 4,7 \right) because PEPE passes through R(4,7)R\left( 4,7 \right) .]
⇒x1(y−7)=x1(x−4)−x+4 ⇒x1(y−x−3)=−(x−4).........(i) \begin{aligned} & \Rightarrow {{x}_{1}}\left( y-7 \right)={{x}_{1}}\left( x-4 \right)-x+4 \\\ & \Rightarrow {{x}_{1}}\left( y-x-3 \right)=-\left( x-4 \right).........\left( i \right) \\\ \end{aligned}
Now, equation of PDPD is given as (y−3)=x1−4x1+4(x−1)\left( y-3 \right)=\dfrac{{{x}_{1}}-4}{{{x}_{1}}+4}\left( x-1 \right) .
[PDPD passes through Q(1,3)Q\left( 1,3 \right) .]
⇒x1(y−3)+4(y−3)=x1(x−1)−4(x−1) ⇒x1(y−x−2)=−(4y+4x−16)............(ii) \begin{aligned} & \Rightarrow {{x}_{1}}\left( y-3 \right)+4\left( y-3 \right)={{x}_{1}}\left( x-1 \right)-4\left( x-1 \right) \\\ & \Rightarrow {{x}_{1}}\left( y-x-2 \right)=-\left( 4y+4x-16 \right)............\left( ii \right) \\\ \end{aligned}
Now, the vertex P(h,k)P\left( h,k \right) satisfies both equations (i)&(ii)\left( i \right)\And \left( ii \right) .
So, equation (i)\left( i \right) becomes x1(k−h−3)=−(h−4).........(iii){{x}_{1}}\left( k-h-3 \right)=-\left( h-4 \right).........\left( iii \right)
And equation (ii)\left( ii \right) becomes x1(k−h−2)=−(4k+4h−16).......(iv){{x}_{1}}\left( k-h-2 \right)=-\left( 4k+4h-16 \right).......\left( iv \right)
Now, on dividing equation (iii)&(iv)\left( iii \right)\And \left( iv \right) , we get;
x1(k−h−3)x1(k−h−2)=−(h−4)−(4k+4h−16)\dfrac{{{x}_{1}}\left( k-h-3 \right)}{{{x}_{1}}\left( k-h-2 \right)}=\dfrac{-\left( h-4 \right)}{-\left( 4k+4h-16 \right)}
⇒(k−h−3)(4k+4h−16)=(h−4)(k−h−2) ⇒4k2+4kh−16k−4kh−4h2+16h−12k−12h+48=kh−h2−2h−4k+4h+8 ⇒4k2−3h2−hk+2h−24k+40=0........(v) \begin{aligned} & \Rightarrow \left( k-h-3 \right)\left( 4k+4h-16 \right)=\left( h-4 \right)\left( k-h-2 \right) \\\ & \Rightarrow 4{{k}^{2}}+4kh-16k-4kh-4{{h}^{2}}+16h-12k-12h+48=kh-{{h}^{2}}-2h-4k+4h+8 \\\ & \Rightarrow 4{{k}^{2}}-3{{h}^{2}}-hk+2h-24k+40=0........(v) \\\ \end{aligned}
Now, to find the locus of P(h,k)P\left( h,k \right) , we will substitute (x,y)(x,y) in place of (h,k)\left( h,k \right) in equation (v)(v) .
So, the locus of P(h,k)P\left( h,k \right) is given as 4y2−3x2−xy+2x−24y+40=04{{y}^{2}}-3{{x}^{2}}-xy+2x-24y+40=0 .
⇒3x2−4y2+xy−2x+24y−40=0\Rightarrow 3{{x}^{2}}-4{{y}^{2}}+xy-2x+24y-40=0
Hence, the locus of P is given by the equation 3x2−4y2+xy−2x+24y−40=03{{x}^{2}}-4{{y}^{2}}+xy-2x+24y-40=0 .
Hence, the correct option is option (c) .

Note : While simplifying the equation take care of sign of terms. These equations can be confusing and sign mistakes are very common. Don’t get confused with orthocenter and circumcentre.