Question
Question: Two vertices of a triangle are (4, –3) and (–2, 5). If the orthocentre of the triangle is at (1, 2),...
Two vertices of a triangle are (4, –3) and (–2, 5). If the orthocentre of the triangle is at (1, 2), then the third vertex is.
A
(– 33, – 26)
B
(33, 26)
C
(26, 33)
D
None of these
Answer
(33, 26)
Explanation
Solution
Let third vertex be (h, k). Now slope of AD is h−1k−2
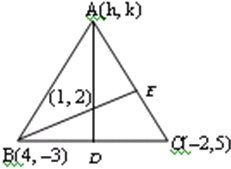
Slope of BC is −2−45+3=3−4
Slope of BE is 4−1−3−2=3−5
And slope of AC is h+2k−5
Since AD⊥BC⇒h−1k−2×3−4=−1
3h−4k+5=0 ......(i)
Again Since BE⊥AC⇒−35×h+2k−5=−1
⇒ 3h−5k+31=0 .....(ii)
on solving (i) and (ii) we get h=33,k=26
Hence the third vertex is (33, 26).
