Solveeit Logo
Login

Question

Question: Two vertices of a triangle are \[(0,2)\] and \[(4,3)\]. If its orthocenter is at the origin, then it...

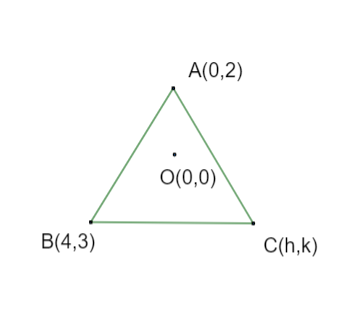
Two vertices of a triangle are (0,2)(0,2) and (4,3)(4,3). If its orthocenter is at the origin, then its third vertex lies in which quadrant?
A. Fourth
B. Second
C. Third
D. First

Explanation

Solution

We must assume the third vertex as (h,k)(h,k), write equation of any two altitudes through two vertices, which should be of the form y−y1=m(x−x1)y - {y_1} = m\left( {x - {x_1}} \right). Since orthocenter is the point of intersection of these two lines i.e. altitudes so it satisfies both these equations. This gives two equations in h and k, which generally looks like mh+nk=pmh + nk = p where m, n, p are constants. If we solve them it will give actual coordinates i.e. (h,k)(h,k) of the third vertex.

Complete step by step answer:
Orthocenter of a triangle is the point of intersection of altitudes of the triangle.
Let us assume the coordinates of the third vertex to be (h,k)(h,k),

Now to find the slope of line perpendicular to AB, we use method given below –
To find the slope (m) of a line having two points (x1,y1)\left( {{x_1},{y_1}} \right) and (x2,y2)\left( {{x_2},{y_2}} \right) we use given formula,
m=y2−y1x2−x1m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}
Hence, slope of AB can be determined by using above formula where slope is denoted by mAB{m_{AB}} :–
Since coordinates of A and B are (0,2)\left( {0,2} \right) and (4,3)\left( {4,3} \right) respectively,
mAB=3−24−0{m_{AB}} = \dfrac{{3 - 2}}{{4 - 0}}
mAB=14{m_{AB}} = \dfrac{1}{4}
We have a unique relation between slopes mm and m⊥{m_ \bot } of two perpendicular lines i.e.
m×m⊥=−1m \times {m_ \bot } = - 1
Now we use this relation to find slope of line perpendicular to AB denoted by,
mAB×m⊥AB=−1{m_{AB}} \times {m_{ \bot AB}} = - 1
m⊥AB=−114{m_{ \bot AB}} = \dfrac{{-1}}{\dfrac{1}{4}}
m⊥AB=−4{m_{ \bot AB}} = - 4
Slope of AC denoted as mAC{m_{AC}} can also be found using the slope-formula stated above –
Using the coordinates of A and B i.e., (0,2)\left( {0,2} \right) and (h,k)\left( {h,k} \right)respectively in order to find the slope using the same slope formula stated above:
mAC=k−2h{m_{AC}} = \dfrac{{k - 2}}{h}
Similarly we can write the relation stated above to find the slope of line perpendicular to AC:
mAC×m⊥AC=−1{m_{AC}} \times {m_{ \bot AC}} = - 1
m⊥AC=−1k−2h{m_{ \bot AC}} = \dfrac{{ - 1}}{{\dfrac{{k - 2}}{h}}}
m⊥AC=h2−k{m_{ \bot AC}} = \dfrac{h}{{2 - k}}
As we know that the equation of a line passing through a point (x′,y′)(x',y') with slope mm is given by:
y−y′=m(x−x′)y - y' = m(x - x')
Similarly, the equation of a line perpendicular to line AC is given below as:
y−3=h2−k(x−4)...(1)y - 3 = \dfrac{h}{{2 - k}}(x - 4)...(1)
And the equation of line perpendicular to line AB is given below as:
y−k=−4(x−h)…(2)y - k = - 4(x - h) \ldots (2)
Since orthocenter is intersection of (1)(1) and (2)(2), and its value is already mentioned in question as (0,0)\left( {0,0} \right),
We put (0,0)(0,0) in both equations, since orthocenter satisfies (1)\left( 1 \right) and (2)\left( 2 \right)
First we put values of x=0,y=0x = 0,y = 0 in equation (1)\left( 1 \right),
0−3=h2−k(0−4)0 - 3 = \dfrac{h}{{2 - k}}(0 - 4)
−3=−4h2−k- 3 = \dfrac{{ - 4h}}{{2 - k}}
3(2−k)=4h3(2 - k) = 4h
4h+3k=6....(3)4h + 3k = 6....(3)
Again we put x=0,y=0x = 0,y = 0 in second equation (2)\left( 2 \right),
0−k=−4(0−h)0 - k = - 4(0 - h)
−k=−4×−h- k = - 4 \times - h
k=−4hk = - 4h
Using both relations
(h,k)=(−34,3)(h,k) = \left( { - \dfrac{3}{4},3} \right)

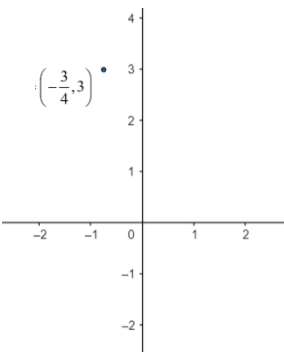
So, the correct answer is “Option B”.

Note: The student must have an idea of what an orthocenter is and also to write equations of line passing through two points and its slope given as y−y′=m(x−x′)y - y' = m(x - x'). The student must be able to identify origin and know how to locate a point on the graph.