Question

Two uniform strings of mass per unit length $\mu$ and $4\mu$, and length $L$ and $2L$, respectively, are joined at point $O$, and tied at two fixed ends $P$ and $Q$, as shown in the figure. The strings are under a uniform tension $T$. If we define the frequency $v_0 = \frac{1}{2L} \sqrt{\frac{T}{\mu}}$, which of the following statements is(are) correct?

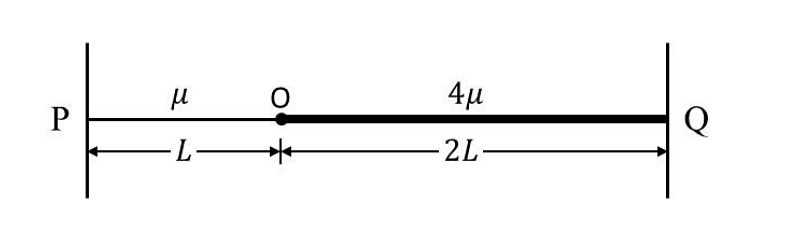
• A. With a node at $O$, the minimum frequency of vibration of the composite string is $v_0$.
• B. With an antinode at $O$, the minimum frequency of vibration of the composite string is $2v_0$.
• C. When the composite string vibrates at the minimum frequency with a node at $O$, it has 6 nodes, including the end nodes
• D. No vibrational mode with an antinode at $O$ is possible for the composite string.

Answer 1

Answer: (A), (C), (D)

With a node at $O$, the minimum frequency of vibration of the composite string is $v_0$.

Answer 2

The correct option is (A): With a node at $O$, the minimum frequency of vibration of the composite string is $v_0$.,(C): When the composite string vibrates at the minimum frequency with a node at $O$, it has 6 nodes, including the end node and (D): No vibrational mode with an antinode at $O$ is possible for the composite string.