Solveeit Logo
Login

Question

Question: Two trees, A and B are on the same side of a river. From a point C in the river the distance of the ...

Two trees, A and B are on the same side of a river. From a point C in the river the distance of the tree A and B is 250 m and 300 m respectively. If the angle C is 450{45^0}, find the distance between the trees (use 2=1.44\sqrt 2 = 1.44).

Explanation

Solution

Hint- Here, we are given two sides and one interior angle of a triangle ABC and we have to find the third side of this triangle. This can be also done by using the cosine rule in the triangle ABC which is (AB)2=(AC)2+(BC)2−2(AC)(BC)cos⁡(∠C){\left( {{\text{AB}}} \right)^2} = {\left( {{\text{AC}}} \right)^2} + {\left( {{\text{BC}}} \right)^2} - 2\left( {{\text{AC}}} \right)\left( {{\text{BC}}} \right)\cos \left( {\angle {\text{C}}} \right)

Complete step-by-step solution -

Let us draw a triangle ABC with points A and B representing two trees on the same side of the river and C is a point in the river as shown in the figure.

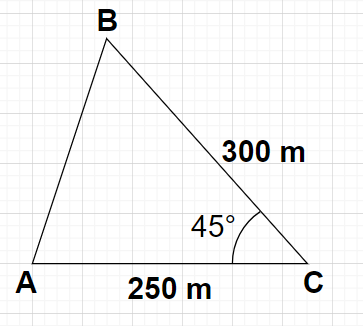
Given, AC = 250 m, BC = 300 m, ∠C=450\angle {\text{C}} = {45^0}
According to cosine rule (for the length AB) applied on any triangle ABC, we can write
(AB)2=(AC)2+(BC)2−2(AC)(BC)cos⁡(∠C) →(1){\left( {{\text{AB}}} \right)^2} = {\left( {{\text{AC}}} \right)^2} + {\left( {{\text{BC}}} \right)^2} - 2\left( {{\text{AC}}} \right)\left( {{\text{BC}}} \right)\cos \left( {\angle {\text{C}}} \right){\text{ }} \to {\text{(1)}}
By substituting AC = 250, BC = 300 and ∠C=450\angle {\text{C}} = {45^0} in equation (1), we get
⇒(AB)2=(250)2+(300)2−2(250)(300)cos⁡(450) →(2)\Rightarrow {\left( {{\text{AB}}} \right)^2} = {\left( {{\text{250}}} \right)^2} + {\left( {{\text{300}}} \right)^2} - 2\left( {{\text{250}}} \right)\left( {{\text{300}}} \right)\cos \left( {{{45}^0}} \right){\text{ }} \to {\text{(2)}}
According to the general trigonometric table,
cos⁡450=12 →(3)\cos {45^0} = \dfrac{1}{{\sqrt 2 }}{\text{ }} \to {\text{(3)}}
By substituting equation (3) in equation (2), we get
⇒(AB)2=62500+90000−150000(12)\Rightarrow {\left( {{\text{AB}}} \right)^2} = 62500 + 90000 - 150000\left( {\dfrac{1}{{\sqrt 2 }}} \right)
Using 2=1.44\sqrt 2 = 1.44, the above equation becomes
(AB)2=62500+90000−150000(11.44) ⇒(AB)2=62500+90000−3125003 ⇒(AB)2=62500+90000−3125003 ⇒(AB)2=1450003  {\left( {{\text{AB}}} \right)^2} = 62500 + 90000 - 150000\left( {\dfrac{1}{{1.44}}} \right) \\\ \Rightarrow {\left( {{\text{AB}}} \right)^2} = 62500 + 90000 - \dfrac{{312500}}{3} \\\ \Rightarrow {\left( {{\text{AB}}} \right)^2} = 62500 + 90000 - \dfrac{{312500}}{3} \\\ \Rightarrow {\left( {{\text{AB}}} \right)^2} = \dfrac{{145000}}{3} \\\
By taking square root on both sides of the above equation, we get
⇒AB=1450003=219.85 m\Rightarrow {\text{AB}} = \sqrt {\dfrac{{145000}}{3}} = 219.85{\text{ m}}
Therefore, the distance between the trees A and B is 219.85 m

Note- In general, there are three cosine rules which can be applied in any triangle ABC. The length AB is given by (AB)2=(AC)2+(BC)2−2(AC)(BC)cos⁡(∠C){\left( {{\text{AB}}} \right)^2} = {\left( {{\text{AC}}} \right)^2} + {\left( {{\text{BC}}} \right)^2} - 2\left( {{\text{AC}}} \right)\left( {{\text{BC}}} \right)\cos \left( {\angle {\text{C}}} \right), the length BC is given by (BC)2=(AB)2+(AC)2−2(AB)(AC)cos⁡(∠A){\left( {{\text{BC}}} \right)^2} = {\left( {{\text{AB}}} \right)^2} + {\left( {{\text{AC}}} \right)^2} - 2\left( {{\text{AB}}} \right)\left( {{\text{AC}}} \right)\cos \left( {\angle {\text{A}}} \right) and the length AC is given by (AC)2=(AB)2+(BC)2−2(AB)(BC)cos⁡(∠B){\left( {{\text{AC}}} \right)^2} = {\left( {{\text{AB}}} \right)^2} + {\left( {{\text{BC}}} \right)^2} - 2\left( {{\text{AB}}} \right)\left( {{\text{BC}}} \right)\cos \left( {\angle {\text{B}}} \right).