Question

Two trains A and B of length 400m each are moving on two parallel tracks with a uniform speed of $72km{{h}^{-1}}$ in the same direction with A ahead of B. The driver of B decides to overtake A and accelerates by $1m{{s}^{-2}}$. If after the 50s, the guard of B just brushes past the driver of A, what was the original distance between them?
A. 100m
B. 1150m
C. 1300m
D. 1250m

Answer 1

As a first step, you could make a rough sketch of the given situation. Thereby you will get better clarity of the given problem and then you could apply the equations of motion by substituting the given information in the question. Also, make sure that all values are in the same units while substituting.
Formula used:
Equation of motion,
$S=ut+\dfrac{1}{2}a{{t}^{2}}$

Complete answer:
In the question we have two trains A and B that have the same length of 400m and initial velocity and the train A leads B by some distance x moving in the same direction. Train B overtakes A by accelerating at $1m{{s}^{-2}}$ after 50s. We are asked to find the initial distance of separation between the two trains.
Let the train B overtake A at some point C.

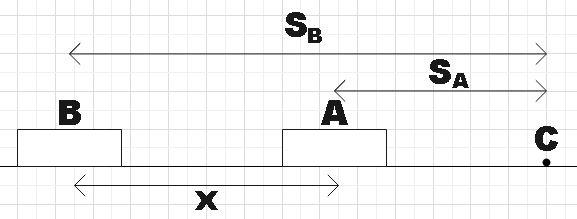
The distance travelled by train A to reach the point C would be given by,
${{S}_{A}}=u\times t=72\times \dfrac{5}{18}\times 50$
$\therefore {{S}_{A}}=1000m$ …………………………………………. (1)
Now the distance travelled by train B to reach that point would be given by,
${{S}_{B}}=ut+\dfrac{1}{2}a{{t}^{2}}$
$\Rightarrow {{S}_{B}}=72\times \dfrac{5}{18}\times 50+\dfrac{1}{2}\times 1\times {{50}^{2}}$
$\therefore {{S}_{B}}=1000+1250=2250m$ …………………………………………. (2)
From the figure above we see that the initial distance of separation of the two trains x is given by the difference of the distances covered by the two trains that is the difference of the two equations (1) and (2).
$x={{S}_{B}}-{{S}_{A}}$
$\Rightarrow x=2250-1000$
$\therefore x=1250m$
Therefore, we found the initial distance of separation of the two trains to be 1250m.

Hence, option D is found to be the correct answer.

Note:
You may have noted that we have multiplied the given value of initial velocity of the two trains by$\dfrac{5}{18}$. This is actually done so as to convert the given value in $km{{h}^{-1}}$ to$m{{s}^{-1}}$.
$1km/h=\dfrac{1000}{3600}m/s=\dfrac{5}{18}m/s$
As the two trains have the same lengths we shouldn’t worry about that while solving.