Question

Two thin wire rings each having a radius R is placed at a distance d apart with their axes coinciding. The charges on the two rings are +q and –q. the potential difference between the centres of the two rings is -

Answer 1

The potential difference across the ring is given as the relation between the charge and the distance between the charge and the point. The potential at the rings A and B will be because of the charges present at both the rings. After computing the same, we will find the difference between the potentials to find the difference between the potentials.

Formula Used
$V=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{R}$

Complete step-by-step solution:
From the given information, we have the data as follows.
Two thin wire rings each having a radius R are placed at a distance d apart with their axes coinciding. The charges on the two rings are +q and –q.
Let the two wire rings be named as A and B.
The potential at the ring A is given by the formula as follows.
${{V}_{A}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{R}+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{(-q)}{\sqrt{{{R}^{2}}+{{d}^{2}}}}$
The potential at the ring B is given by the formula as follows.
${{V}_{B}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{(-q)}{R}+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{\sqrt{{{R}^{2}}+{{d}^{2}}}}$

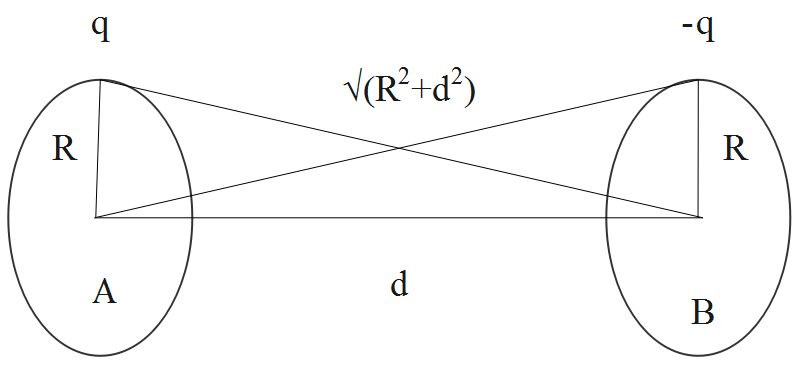
Therefore, the potential difference between the thin wire rings A and B is given as follows.
$V={{V}_{A}}-{{V}_{B}}$
Substitute the expressions of the potentials at the rings A and B that we have obtained in the above equation.
$V=\left( \dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{R}+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{(-q)}{\sqrt{{{R}^{2}}+{{d}^{2}}}} \right)-\left( \dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{(-q)}{R}+\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{\sqrt{{{R}^{2}}+{{d}^{2}}}} \right)$
Continue further computation and take out the common terms.
$\Rightarrow V=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\left[ \dfrac{q}{R}+\dfrac{q}{R}-\dfrac{q}{\sqrt{{{R}^{2}}+{{d}^{2}}}}-\dfrac{q}{\sqrt{{{R}^{2}}+{{d}^{2}}}} \right]$
Therefore, the value of the potential difference between the centers of the two rings is,
$\therefore V=\dfrac{q}{2\pi {{\varepsilon }_{0}}}\left[ \dfrac{1}{R}-\dfrac{1}{\sqrt{{{R}^{2}}+{{d}^{2}}}} \right]$
$\therefore$The potential difference between the centers of the two rings is$\dfrac{q}{2\pi {{\varepsilon }_{0}}}\left[ \dfrac{1}{R}-\dfrac{1}{\sqrt{{{R}^{2}}+{{d}^{2}}}} \right]$, thus, option (B) is correct.

Note: The potential difference because of the potentials at the rings will be computed based on the sign of the charge. If, one of the charges gets a negative sign, then, the potential difference will be computed as the sum of the potentials, otherwise, the potential difference will be computed as the difference between the potentials.