Question

Two thin rods of length $L$ lie along x-axis, one between $x=\dfrac{a}{2}$ to $x=\dfrac{a}{2}+L$ and other between $x=-\dfrac{a}{2}$ to $x=-\dfrac{a}{2}-L$ .
Each rod has positive charge $Q$ distributed uniformly along the length. Find the magnitude of the force which one rod exerts on the other.
$\begin{aligned} & \text{A}\text{. }\dfrac{{{Q}^{2}}}{4\pi {{\epsilon }_{0}}{{L}^{2}}}{{\log }_{e}}\dfrac{L-a}{L+a} \\\ & \text{B}\text{. }\dfrac{{{Q}^{2}}}{4\pi {{\epsilon }_{0}}{{L}^{2}}}{{\log }_{e}}a\dfrac{{{\left( L+a \right)}^{2}}}{\left( L-a \right)} \\\ & \text{C}\text{. }\dfrac{{{Q}^{2}}}{4\pi {{\epsilon }_{0}}{{L}^{2}}}{{\log }_{e}}\dfrac{{{\left( L+a \right)}^{2}}}{a\left( 2L+a \right)} \\\ & \text{D}\text{. }\dfrac{{{Q}^{2}}}{4\pi {{\epsilon }_{0}}{{L}^{2}}}{{\log }_{e}}\dfrac{{{\left( L+a \right)}^{2}}}{L\left( L+2a \right)} \\\ \end{aligned}$

Answer 1

First calculate the electric field due to the second rod at any point on its axis . then calculate the force due to the second rod on a small element on the first rod. And then integrate it over the full rod to get the force.

Formulas used:
Linear charge density is defined as the charge per unit length, $\lambda =\dfrac{Q}{L}$
Electric field due to a small element $dx$ of rod having linear charge density $\lambda$ at a point $r$ is
$dE=\dfrac{1}{4\pi {{\epsilon }_{0}}}\int{\dfrac{\lambda dx}{{{r}^{2}}}}$
The total electric field will be given by integrating over whole rod
$E=\dfrac{1}{4\pi {{\epsilon }_{0}}}\int\limits_{0}^{L}{\dfrac{\lambda dx}{{{r}^{2}}}}$
Force on an element of charge $dq$ due to the electric field $E$ is
$F=dq\times E$
$\int{\dfrac{1}{x+p}dx=\ln \left( x+p \right)+c}$
$\ln p-\ln q=\ln \dfrac{p}{q}$ , and
$\ln p+\ln q=\ln \left( pq \right)$

Complete step by step answer:
Linear charge density of both the rods is , $\lambda =\dfrac{Q}{L}$
From the figure The electric field $dE$ at a point P situated at a distance $r$ from the origin at x-axis due to element of charge $dq$in second rod is given by
$dE=\dfrac{1}{4\pi {{\epsilon }_{0}}}\int{\dfrac{\lambda dx}{{{\left( -x+r \right)}^{2}}}}$

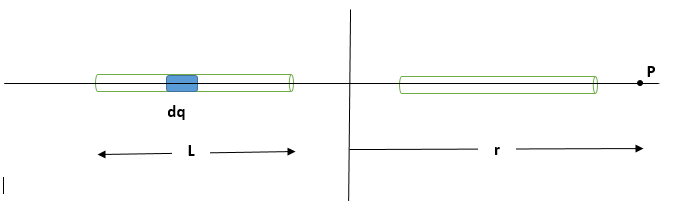
The field due to the whole rod at point P is given by integrating the charge element over the whole rod and is given by

& E=\dfrac{1}{4\pi {{\epsilon }_{0}}}\times \dfrac{Q}{L}\int\limits_{-\dfrac{a}{2}-L}^{-\dfrac{a}{2}}{\dfrac{dx}{{{\left( -x+r \right)}^{2}}}} \\\ & \Rightarrow E=\dfrac{Q}{4\pi {{\epsilon }_{0}}L}\left[ \dfrac{{{\left( -x+r \right)}^{-2+1}}}{-2+1}\left( -1 \right) \right]_{-\dfrac{a}{2}-L}^{-\dfrac{a}{2}} \\\ & \Rightarrow E=\dfrac{Q}{4\pi {{\epsilon }_{0}}L}\left[ \dfrac{1}{-x+r} \right]_{-\dfrac{a}{2}-L}^{-\dfrac{a}{2}} \\\ & \Rightarrow E=\dfrac{Q}{4\pi {{\epsilon }_{0}}L}\left[ \dfrac{1}{-\left( -\dfrac{a}{2} \right)+r}-\dfrac{1}{-\left( -\dfrac{a}{2}-L \right)+r} \right] \\\ & \Rightarrow E=\dfrac{Q}{4\pi {{\epsilon }_{0}}L}\left[ \dfrac{1}{\dfrac{a}{2}+r}-\dfrac{1}{r+\dfrac{a}{2}+L} \right] \\\ \end{aligned}$$ Now force on a charge element of first rod by the second rod which is at a distance $x$ from the rod is  $dF=dq\times E=\lambda dx\times E=\lambda dx\times \dfrac{Q}{4\pi {{\epsilon }_{0}}L}\left[ \dfrac{1}{\dfrac{a}{2}+x}-\dfrac{1}{x+\dfrac{a}{2}+L} \right]$ The net force on the first rod due to second rod can be by integrating $dF$ over the whole first rod. So $$\begin{aligned} & F=\int\limits_{\dfrac{a}{2}}^{\dfrac{a}{2}+L}{\lambda dx\times \dfrac{Q}{4\pi {{\epsilon }_{0}}L}\left[ \dfrac{1}{\dfrac{a}{2}+x}-\dfrac{1}{x+\dfrac{a}{2}+L} \right]} \\\ & \Rightarrow F=\int\limits_{\dfrac{a}{2}}^{\dfrac{a}{2}+L}{\dfrac{Q}{L}\times \dfrac{Q}{4\pi {{\epsilon }_{0}}L}\left[ \dfrac{1}{\dfrac{a}{2}+x}-\dfrac{1}{x+\dfrac{a}{2}+L} \right]}dx\left( \because \lambda =\dfrac{Q}{L} \right) \\\ & \Rightarrow F=\int\limits_{\dfrac{a}{2}}^{\dfrac{a}{2}+L}{\dfrac{{{Q}^{2}}}{4\pi {{\epsilon }_{0}}{{L}^{2}}}\left[ \dfrac{1}{\dfrac{a}{2}+x}-\dfrac{1}{x+\dfrac{a}{2}+L} \right]}dx \\\ & \Rightarrow F=\dfrac{{{Q}^{2}}}{4\pi {{\epsilon }_{0}}{{L}^{2}}}\left[ \ln \left( x+\dfrac{a}{2} \right)-\ln \left( x+L+\dfrac{a}{2} \right) \right]_{\dfrac{a}{2}+L}^{\dfrac{a}{2}+L} \\\ \end{aligned}$$ Because $\int{\dfrac{1}{x+p}dx=\ln \left( x+p \right)+c}$ Putting the limits $$\begin{aligned} & F=\dfrac{{{Q}^{2}}}{4\pi {{\epsilon }_{0}}{{L}^{2}}}\left[ \ln \left( \dfrac{a}{2}+L+\dfrac{a}{2} \right)-\ln \left( \dfrac{a}{2}+L+L+\dfrac{a}{2} \right)-\left\\{ \ln \left( \dfrac{a}{2}+\dfrac{a}{2} \right)-\ln \left( \dfrac{a}{2}+L+\dfrac{a}{2} \right) \right\\} \right] \\\ & \Rightarrow F=\dfrac{{{Q}^{2}}}{4\pi {{\epsilon }_{0}}{{L}^{2}}}\left[ \ln \left( a+L \right)-\ln \left( a+2L \right)-\ln a+\ln \left( a+L \right) \right] \\\ & \Rightarrow F=\dfrac{{{Q}^{2}}}{4\pi {{\epsilon }_{0}}{{L}^{2}}}\ln \left[ \dfrac{{{\left( a+L \right)}^{2}}}{a\left( a+2L \right)} \right] \\\ \end{aligned}$$ Because, $\ln p-\ln q=\ln \dfrac{p}{q}\text{ and }\ln p+\ln q=\ln \left( pq \right)$ **So the correct option is Option .C** **Note:** In problems like this see the charge distribution. Whether the charge is distributed over volume or surface area or the length. If the charge is distributed over volume then use volume charge density. If the charge is distributed over the surface then use surface charge density. Igf the charge is distributed over length then use linear charge density. After calculating the charge density you can calculate the electric field or force due to this small element of charge then integrate it to get total Electric field and also total force.