Question

Two thin discs, each of mass $M$ and radius $\;r\;$ meter, are attached as shown in the fig. to form a rigid body. The rotational inertia of this body about an axis perpendicular to the plane of disc $B$ passing through its center is

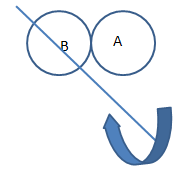
(A) $2M{r^2}$
(B) $3M{r^2}$
(C) $4M{r^2}$
(D) $5M{r^2}$

Answer 1

Given that two thin discs have the same mass and radius attached to form a rigid body. We need to find the moment of inertia of the disc $B$ about an axis perpendicular to the plane of the disc $B$ passing through its center. For that, we need to find the moment of inertia of disc $B$ which is equal to the sum of moment of inertia of disc $B$ about its center and moment of inertia of disc $A$ about $B$ .

Complete Step By Step Answer:
Two thin discs having mass $M$ and radius $\;r\;$ meter.
To start with, we need to find the moment of inertia of the disc $B$
${I_B} = {I_B}' + {I_A}$ ……… (1)
Here ${I_B}$ is the total moment of inertia of the disc $B$
${I_B}'$ is known as the moment of inertia of disc $B$ about its center
${I_A}$ is a quantity that describes the moment of inertia of the disc $A$
We already know the moment of inertia of disc $B$ about its center which is given by,
${I_B}' = \dfrac{{M{r^2}}}{2}$
Here $M$ is the mass of the disc $B$ and $r$ is the radius of the disc $B$ .
Now to find the moment of inertia of the disc $A$ we need to use the parallel axis theorem.
The parallel axis theorem states that the moment of inertia of a body passing via the center of mass is equivalent to the sum of the moment of inertia of the body passing via the center of mass and the product of the mass of the body times square of the distance between them.
${I_A}{\text{ }} = {\text{ }}{I_A}'\; + {\text{ }}M{h^2}$
Where,
${I_A}$ is known as the moment of inertia of the disc $A$
${I_A}'$ is known as the moment of inertia about the center of the disc $A$
$M$ is known as the mass of the disc
${h^2}$ is known as the square of the distance between the two axes.
Now the moment of inertia about the center of the disc $A$ is given by,
${I_A}'$ $= \dfrac{{M{r^2}}}{2}$
We know the radius is $\;r\;$ for each disc, therefore square of the distance between the two axes is ${(2r)^2}$
Now substituting all these values in parallel axis theorem we get,
${I_A}{\text{ }} = \dfrac{{M{r^2}}}{2}\; + {(2r)^2} = 9M{r^2}$
Thus we got an expression for both ${I_B}'$ and ${I_A}$ we can substitute this in equation (1)
Now the total moment of inertia the body about an axis perpendicular to the plane of disc $B$ passing through its center is
${I_B} = {I_B}' + {I_A}$
${I_B} = \dfrac{{M{r^2}}}{2} + 9M{r^2}$
${I_B} = 5M{r^2}$
Therefore the correct option is D.

Note:
The Moment of inertia is defined as the property of anybody due to which it resists angular acceleration, which is the sum of all the products of the mass of every individual particle in the body with the square of its distance from the axis of rotation.
Moment of inertia $\;I{\text{ }} = \;\Sigma {\text{ }}{m_i}{r_i}^2$
To calculate this moment of inertia we have another important theorem in addition to the parallel axis theorem that is the perpendicular axis theorem.