Question

Two tangents to a parabola intercept on a fixed tangent segment whose product is a constant. Prove that the locus of their point of intersection is a straight line.

Answer 1

Hint: The general equation of tangent at $\left( a{{t}^{2}},2at \right)$is given by $ty=x+a{{t}^{2}}$, where $t$ is a parameter .
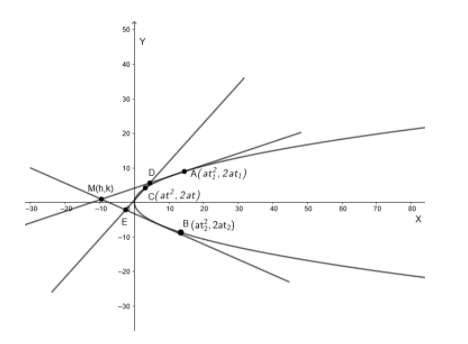
The point of intersection of tangents at $A\left( at_{1}^{2},2a{{t}_{1}} \right)$and $B\left( at_{2}^{2},2a{{t}_{2}} \right)$ is given by $\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$, where ${{t}_{1}}$ and ${{t}_{2}}$ are parameters.

We will consider the equation of the parabola to be ${{y}^{2}}=4ax$.
We will consider two points $A\left( at_{1}^{2},2a{{t}_{1}} \right)$ and $B\left( at_{2}^{2},2a{{t}_{2}} \right)$ on the parabola , where ${{t}_{1}}$ and ${{t}_{2}}$ are parameters.

Now , we will find the equation of tangents at these points.
Now, we know the general equation of tangent at $\left( a{{t}^{2}},2at \right)$ is given by $ty=x+a{{t}^{2}}$, where $t$ is a parameter .
So , the equation of tangent at $A\left( at_{1}^{2},2a{{t}_{1}} \right)$ is given by substituting ${{t}_{1}}$ in place of $t$ in the general equation of tangent .
On substituting ${{t}_{1}}$ in place of $t$ in the general equation of tangent , we get
${{t}_{1}}y=x+at_{1}^{2}.....\left( i \right)$
And equation of tangent at $B\left( at_{2}^{2},2a{{t}_{2}} \right)$ is given as
${{t}_{2}}y=x+at_{2}^{2}....\left( ii \right)$
Now, we need to find the locus of the point of intersection of $\left( i \right)$and $\left( ii \right)$.
Let the point of intersection be $M\left( h,k \right)$.
Now, from equation$\left( i \right)$, we have
$y{{t}_{1}}=x+at_{1}^{2}$
$\Rightarrow x={{t}_{1}}\left( y-a{{t}_{1}} \right).....\left( iii \right)$
We will substitute the value of $x$ from equation $(iii)$ in equation $\left( ii \right)$.
On substituting value of $x$ from equation$(iii)$ in equation $\left( ii \right)$, we get,
$y{{t}_{2}}={{t}_{1}}y-at_{1}^{2}+at_{2}^{2}$
$\Rightarrow y\left( {{t}_{2}}-{{t}_{1}} \right)=a\left( t_{2}^{2}-t_{1}^{2} \right)$
$\Rightarrow y=a\left( {{t}_{1}}+{{t}_{2}} \right)$
Substituting $y=a\left( {{t}_{1}}+{{t}_{2}} \right)$in $\left( iii \right)$, we get
$x={{t}_{1}}\left( a{{t}_{1}}+a{{t}_{2}}-a{{t}_{1}} \right)$
$\Rightarrow x=a\left( {{t}_{1}}{{t}_{2}} \right)$
So, the point of intersection of tangents $\left( i \right)$ and $\left( ii \right)$ is $\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$.
Comparing it with$M\left( h,k \right)$, we get
$h=a{{t}_{1}}{{t}_{2}}$
$\Rightarrow \dfrac{h}{a}={{t}_{1}}{{t}_{2}}.....\left( iv \right)$
And $k=a\left( {{t}_{1}}+{{t}_{2}} \right)$
$\Rightarrow \dfrac{k}{a}={{t}_{1}}+{{t}_{2}}.....\left( v \right)$
Now, we will consider the point of contact of the fixed tangent be $C\left( a{{t}^{2}},2at \right)$.
So , the point of intersection of tangent at $A$ and tangent at $C$ is $D\left( at{{t}_{1}},a\left( t+{{t}_{1}} \right) \right)$.
And the point of intersection of tangent at $B$ and tangent at $C$ is $E\left( at{{t}_{2}},a\left( t+{{t}_{2}} \right) \right)$.
Now, in the question it is given that the product of intercept on the fixed tangent is constant.
So, $CD\times CE=C$
$\Rightarrow \sqrt{{{\left( a{{t}^{2}}-at{{t}_{1}} \right)}^{2}}+{{\left( 2at-a{{t}_{1}}-at \right)}^{2}}}\times \sqrt{{{\left( a{{t}^{2}}-at{{t}_{2}} \right)}^{2}}+{{\left( 2at-a{{t}_{2}}-at \right)}^{2}}}=C$
$\Rightarrow \sqrt{{{a}^{2}}{{t}^{2}}{{\left( t-{{t}_{1}} \right)}^{2}}+{{a}^{2}}{{\left( t-{{t}_{1}} \right)}^{2}}}\times \sqrt{{{a}^{2}}{{t}^{2}}{{\left( t-{{t}_{2}} \right)}^{2}}+{{a}^{2}}{{\left( t-{{t}_{2}} \right)}^{2}}}=C$
$\Rightarrow a\left( t-{{t}_{1}} \right)\sqrt{{{t}^{2}}+1}\times a\left( t-{{t}_{2}} \right)\sqrt{{{t}^{2}}+1}=C$
$\Rightarrow \left( t-{{t}_{1}} \right)\left( t-{{t}_{2}} \right)=\dfrac{C}{{{a}^{2}}\left( {{t}^{2}}+1 \right)}$
$\Rightarrow \left( t-{{t}_{1}} \right)\left( t-{{t}_{2}} \right)={{C}_{1}}$ (say)
$\Rightarrow {{t}^{2}}-\left( {{t}_{1}}+{{t}_{2}} \right)+{{t}_{1}}{{t}_{2}}={{C}_{1}}....\left( vi \right)$
Substituting $\left( iv \right)$and $\left( v \right)$in $\left( vi \right)$, we get
${{t}^{2}}-\dfrac{k}{a}+\dfrac{h}{a}={{C}_{1}}$
$\Rightarrow h-k=a\left( {{C}_{1}}-{{t}^{2}} \right).......(vii)$
Now, to find the locus of $M\left( h,k \right)$, we will substitute $(x,y)$ in place of $(h,k)$ in equation$(vii)$.
So , the locus of $M\left( h,k \right)$ is given as
$x-y=a\left( {{C}_{1}}-{{t}^{2}} \right)$ which represents a straight line.
Note: : While simplifying the equations , please make sure that sign mistakes do not occur. These mistakes are very common and can cause confusions while solving. Ultimately the answer becomes wrong. So, sign conventions should be carefully taken .