Question

Two tangents on a parabola are $x-y=0$ and $x+y=0$, if B (2, 3) is the focus of the parabola. If P and Q are the ends of the focal chord then $\dfrac{1}{\left| BP \right|}+\dfrac{1}{\left| BQ \right|}=$
(a) $\dfrac{2\sqrt{13}}{3}$
(b) $2\sqrt{13}$
(c) $\dfrac{2\sqrt{13}}{5}$
(d) $\dfrac{2\sqrt{13}}{7}$

Answer 1

In this question, first we will figure out the intersection point of the two tangents. Next step, is to find the foot of perpendicular of the focus for the first tangent equation, $\dfrac{x-{{x}_{1}}}{a}=\dfrac{y-{{y}_{1}}}{b}=-\left( \dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{{{a}^{2}}+{{b}^{2}}} \right)$. Similarly, find using the focus and the second tangent equation. Next step, is to find the equation of the line with the help of two obtained points using two-point slope form,$y-{{y}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right)$. Now, using the equation of the tangent at the vertex and the focus, find the length of the latus rectum. Now, the final result is equal to $\dfrac{1}{a}$, hence using some basic mathematical operations to find the required result.

Complete step by step answer:
Here, we have been given two tangents whose equations are $x-y=0$ and $x+y=0$ of the parabola. The focus of the parabola is given as B (2, 3) which will give us a focal chord PQ.
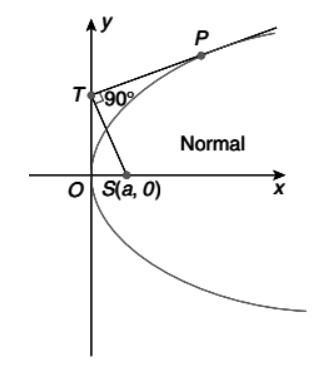
If we observe the equations of the tangents, we can say that they intersect each other at (0,0) creating an angle of $90{}^\circ$.
We know,
The foot of perpendicular from the focus upon a tangent lies on the tangent at the vertex of the parabola.
The representation of the above statement is

We know,
Foot of the perpendicular of $\left( {{x}_{1}},{{y}_{1}} \right)$ for line $ax+by+c=0$ is given by
$\dfrac{x-{{x}_{1}}}{a}=\dfrac{y-{{y}_{1}}}{b}=-\left( \dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{{{a}^{2}}+{{b}^{2}}} \right)$
Now, we have the tangent $x-y=0$, the foot of the perpendicular from the focus B (2, 3) to this tangent is $\left( {{l}_{1}},\,{{m}_{1}} \right)$, we get
$\dfrac{{{l}_{1}}-2}{1}=\dfrac{{{m}_{1}}-3}{-1}=\dfrac{-\left[ \left( 1 \right)\left( 2 \right)+\left( -1 \right)\left( 3 \right)+0 \right]}{{{\left( 1 \right)}^{2}}+{{\left( -1 \right)}^{2}}}$
$\Rightarrow \dfrac{{{l}_{1}}-2}{1}=\dfrac{{{m}_{1}}-3}{-1}=\dfrac{-\left( 2-3 \right)}{2}$
$\Rightarrow \dfrac{{{l}_{1}}-2}{1}=\dfrac{{{m}_{1}}-3}{-1}=\dfrac{1}{2}$
Now, we get
$\begin{aligned} & \Rightarrow \dfrac{{{l}_{1}}-2}{1}=\dfrac{1}{2} \\\ & \Rightarrow {{l}_{1}}-2=\dfrac{1}{2} \\\ & \Rightarrow {{l}_{1}}=\dfrac{1}{2}+2 \\\ & =\dfrac{1}{2}+\dfrac{2\times 2}{1\times 2} \\\ & =\dfrac{1}{2}+\dfrac{4}{2} \\\ & =\dfrac{5}{2} \end{aligned}$
Similarly, we will get ${{m}_{1}}$
$\Rightarrow -{{m}_{1}}+3=\dfrac{1}{2}$
$\Rightarrow \dfrac{{{m}_{1}}-3}{-1}=\dfrac{1}{2}$
$\begin{aligned} & \Rightarrow 3-\dfrac{1}{2}={{m}_{1}} \\\ & \Rightarrow \dfrac{3\times 2}{1\times 2}-\dfrac{1}{2}={{m}_{1}} \\\ &\Rightarrow \dfrac{6}{2}-\dfrac{1}{2}={{m}_{1}} \\\ & \Rightarrow {{m}_{1}}=\dfrac{5}{2} \end{aligned}$
Therefore, $\left( {{l}_{1}},{{m}_{1}} \right)=\left( \dfrac{5}{2},\dfrac{5}{2} \right)$
Now, let us find the foot of the perpendicular $\left( {{l}_{2}},{{m}_{2}} \right)$ from the focus to the tangent $x+y=0$.
$\begin{aligned} & \Rightarrow \dfrac{{{l}_{2}}-2}{1}=\dfrac{{{m}_{2}}-3}{1}=\dfrac{-\left[ \left( 1 \right)\left( 2 \right)+\left( 1 \right)\left( 3 \right)+0 \right]}{{{\left( 1 \right)}^{2}}+{{\left( 1 \right)}^{2}}} \\\ & \dfrac{{{l}_{2}}-2}{1}=\dfrac{{{m}_{2}}-3}{1}=\dfrac{-\left( 2+3 \right)}{2} \\\ & \dfrac{{{l}_{2}}-2}{1}=\dfrac{{{m}_{2}}-3}{1}=\dfrac{-5}{2} \\\ \end{aligned}$
Now, we get
$\begin{aligned} & \dfrac{{{l}_{2}}-2}{1}=\dfrac{-5}{2} \\\ & {{l}_{2}}=\dfrac{-5}{2}+2 \\\ & =\dfrac{-5}{2}+\dfrac{2\times 2}{1\times 2} \\\ & =\dfrac{-5}{2}+\dfrac{4}{2} \\\ & =\dfrac{-5+4}{2} \\\ & =\dfrac{-1}{2} \end{aligned}$
Similarly, we get
$\dfrac{{{m}_{2}}-3}{1}=\dfrac{-5}{2}$
${{m}_{2}}-3=\dfrac{-5}{2}$

& \Rightarrow {{m}_{2}}=\dfrac{-5}{2}+3 \\\ & \Rightarrow {{m}_{2}}=\dfrac{-5}{2}+\dfrac{3\times 2}{1\times 2} \\\ & =\dfrac{-5+6}{2} \\\ & =\dfrac{1}{2} \end{aligned}$$ Therefore, $\left( {{l}_{2}},{{m}_{2}} \right)=\left( \dfrac{-1}{2},\,\dfrac{1}{2} \right)$. Let us create an equation of the tangent at the vertex which passes through the points $\left( \dfrac{5}{2},\dfrac{5}{2} \right)$ and $\left( \dfrac{-1}{2},\,\dfrac{1}{2} \right)$. We know, Two-point slope, $y-{{y}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right)$, we get $\begin{aligned} & \Rightarrow y-\dfrac{5}{2}=\dfrac{\dfrac{1}{2}-\dfrac{5}{2}}{\dfrac{-1}{2}-\dfrac{5}{2}}\left( x-\dfrac{5}{2} \right) \\\ & \Rightarrow y-\dfrac{5}{2}=\dfrac{\dfrac{1-5}{2}}{\dfrac{-1-5}{2}}\left( x-\dfrac{5}{2} \right) \\\ & \Rightarrow y-\dfrac{5}{2}=\dfrac{\dfrac{-4}{2}}{\dfrac{-6}{2}}\left( x-\dfrac{5}{2} \right) \\\ & \Rightarrow y-\dfrac{5}{2}=\dfrac{-2}{-3}\left( x-\dfrac{5}{2} \right) \end{aligned}$ $\begin{aligned} & \Rightarrow y-\dfrac{5}{2}=\dfrac{2x}{3}-\dfrac{5}{3} \\\ & \Rightarrow y-\dfrac{2x}{3}=\dfrac{5}{2}-\dfrac{5}{3} \end{aligned}$ $\begin{aligned} & \Rightarrow \dfrac{y\times 3}{1\times 3}-\dfrac{2x}{3}=\dfrac{5\times 3}{2\times 3}-\dfrac{5\times 2}{3\times 2} \\\ & \Rightarrow \dfrac{3y}{3}-\dfrac{2x}{3}=\dfrac{15}{6}-\dfrac{10}{6} \end{aligned}$ $\begin{aligned} & \Rightarrow \dfrac{3y-2x}{3}=\dfrac{15-10}{6} \\\ & \Rightarrow \dfrac{3y-2x}{3}=\dfrac{5}{6} \end{aligned}$ Now, let us multiply 6 on both the sides of the equation, we get $\begin{aligned} & \Rightarrow 6\times \dfrac{\left( 3y-2x \right)}{3}=\dfrac{5}{6}\times 6 \\\ & \Rightarrow 2\left( 3y-2x \right)=5 \\\ & \Rightarrow 6y-4x=5 \\\ & \Rightarrow 4x-6y+5=0 \end{aligned}$ $4x-6y+5=0$ Now, let us find the length of the latus rectum of the parabola We know, Length of the latus rectum = 4a where, a = distance from focus to the tangent at vertex We get, Length of the latus rectum = $4\times $ (Distance from focus to the tangent at vertex) We know, From distance formula, we get $d=\left| \dfrac{ax+by+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|$ Distance from focus to the tangent at vertex $=\left| \dfrac{\left( 4 \right)\left( 2 \right)+\left( -6 \right)\left( 3 \right)+5}{\sqrt{{{\left( 4 \right)}^{2}}+{{\left( -6 \right)}^{2}}}} \right|$ $$=\left| \dfrac{8-18+5}{\sqrt{16+36}} \right|$$ $=\left| \dfrac{-5}{\sqrt{52}} \right|$ $a=\dfrac{5}{2\sqrt{13}}$ Length of the latus rectum $=4\times a$ $=4\times \dfrac{5}{2\sqrt{13}}$ $\begin{aligned} & =\dfrac{2\times 5}{\sqrt{13}} \\\ & =\dfrac{10}{\sqrt{13}} \\\ \end{aligned}$ We know, that $\dfrac{1}{\left| BP \right|}+\dfrac{1}{\left| BQ \right|}=\dfrac{1}{a}$ In the above equation, we can say that $a$ is the $\dfrac{1}{4}\text{th}$ of the length of the latus rectum, we get $\begin{aligned} & \dfrac{1}{\left| BP \right|}+\dfrac{1}{\left| BQ \right|}=\dfrac{1}{\dfrac{5}{2\sqrt{13}}} \\\ & =\dfrac{2\sqrt{13}}{5} \end{aligned}$ Hence, the required value is $\dfrac{2\sqrt{13}}{5}$.  **Note:** A parabola is a two-dimensional, minor symmetrical curve, it is as a conic section created from the intersection of a right circular conical surface and a plane. The chord passing through the focus and perpendicular to the axis is called latus rectum of conic section.