Question

Two tangents on a parabola are $x+y=0$ and $x-y=0$ . If $\left( 2,3 \right)$ is the focus of parabola then the length of latus rectum of the parabola is
(a) $\dfrac{6}{\sqrt{3}}$
(b) $\dfrac{10}{\sqrt{13}}$
(c) $\dfrac{2}{\sqrt{13}}$
(d) $\dfrac{9\sqrt{2}}{\sqrt{13}}$

Answer 1

The diagram of given data is

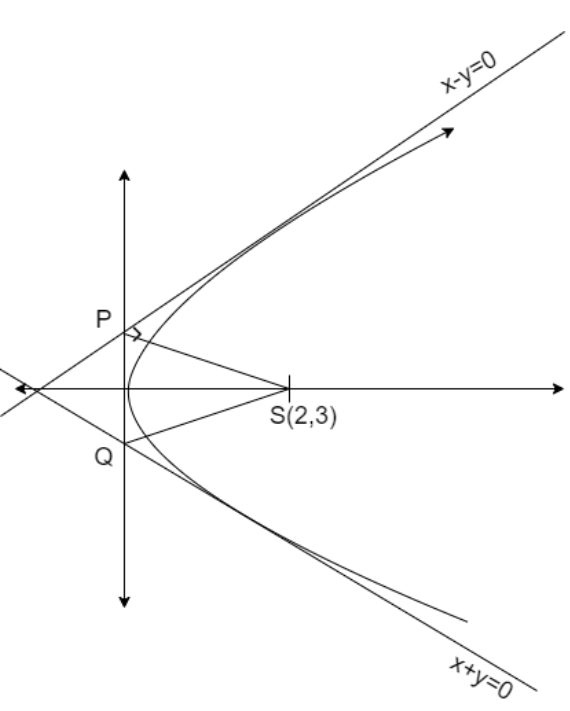
We solve this problem by using the standard result that is the length of the latus rectum is equal to four times the perpendicular distance from the focus to the tangent at a vertex that is
$\Rightarrow \text{Latus rectum}=4\times \left( \text{perpendicular distance from focus to tangent at vertex} \right)$
For finding the tangent at the vertex we use the result that the foot of perpendicular of focus on the tangent lies on the tangent at the vertex. For finding the foot of perpendicular of point $\left( h,k \right)$ on the line $ax+by+c=0$ is given as
$\Rightarrow \dfrac{{{x}_{1}}-h}{a}=\dfrac{{{y}_{1}}-k}{b}=\dfrac{-\left( ah+bk+c \right)}{{{a}^{2}}+{{b}^{2}}}$
We find both feet of perpendicular of focus to both tangents to find the equation of the tangent at a vertex to find the perpendicular distance from the focus to a tangent at a vertex.

Complete step-by-step solution:
Let us assume that the focus as
$\Rightarrow S=\left( 2,3 \right)$
We are given that the two equations of tangents are
$\Rightarrow x+y=0$
$\Rightarrow x-y=0$
We know that the foot of the perpendicular of focus on the tangent lies on the tangent at the vertex.
Now, let us find the foot of perpendicular of focus on tangent $x+y=0$ that is $P\left( {{x}_{1}},{{y}_{1}} \right)$
We know that the foot of perpendicular of point $\left( h,k \right)$ on the line $ax+by+c=0$ is given as
$\Rightarrow \dfrac{{{x}_{1}}-h}{a}=\dfrac{{{y}_{1}}-k}{b}=\dfrac{-\left( ah+bk+c \right)}{{{a}^{2}}+{{b}^{2}}}$
By using the above formula we get
$\Rightarrow \dfrac{{{x}_{1}}-2}{1}=\dfrac{{{y}_{1}}-3}{1}=\dfrac{-\left( 2+3 \right)}{{{1}^{2}}+{{1}^{2}}}$
Now, let us separate the terms then we get

& \Rightarrow \dfrac{{{x}_{1}}-2}{1}=\dfrac{-5}{2} \\\ & \Rightarrow {{x}_{1}}=-\dfrac{1}{2} \\\ \end{aligned}$$ Now, separating the y co – ordinate we get $$\begin{aligned} & \Rightarrow \dfrac{{{y}_{1}}-3}{1}=\dfrac{-5}{2} \\\ & \Rightarrow {{y}_{1}}=\dfrac{1}{2} \\\ \end{aligned}$$ Therefore the point P is $$\left( -\dfrac{1}{2},\dfrac{1}{2} \right)$$ Now let us find the foot of perpendicular of focus on the line $$x-y=0$$ that is $$Q\left( {{x}_{2}},{{y}_{2}} \right)$$ By using the foot of perpendicular formula we get $$\Rightarrow \dfrac{{{x}_{2}}-2}{1}=\dfrac{{{y}_{2}}-3}{-1}=\dfrac{-\left( 2-3 \right)}{{{1}^{2}}+{{1}^{2}}}$$ Now, let us separate the terms then we get $$\begin{aligned} & \Rightarrow \dfrac{{{x}_{2}}-2}{1}=\dfrac{1}{2} \\\ & \Rightarrow {{x}_{2}}=\dfrac{5}{2} \\\ \end{aligned}$$ Now, separating the y co – ordinate we get $$\begin{aligned} & \Rightarrow \dfrac{{{y}_{2}}-3}{-1}=\dfrac{1}{2} \\\ & \Rightarrow {{y}_{2}}=\dfrac{5}{2} \\\ \end{aligned}$$ Therefore the point Q is $$\left( \dfrac{5}{2},\dfrac{5}{2} \right)$$ Now, let us find the equation of line PQ We know that the equation of line having the points $$\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$$ is given as $$\Rightarrow y-{{y}_{1}}=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)\left( x-{{x}_{1}} \right)$$ Now by substituting the required values in above equation we get $$\begin{aligned} & \Rightarrow y-\dfrac{1}{2}=\left( \dfrac{\dfrac{5}{2}-\dfrac{1}{2}}{\dfrac{5}{2}-\left( -\dfrac{1}{2} \right)} \right)\left( x+\dfrac{1}{2} \right) \\\ & \Rightarrow y-\dfrac{1}{2}=\dfrac{2}{3}\left( x+\dfrac{1}{2} \right) \\\ & \Rightarrow 4x-6y+5=0 \\\ \end{aligned}$$ We know that the length of latus rectum is equal to four times the perpendicular distance from focus to tangent at vertex that is $$\Rightarrow \text{Latus rectum}=4\times \left( \text{perpendicular distance from focus to tangent at vertex} \right)$$ Now, by using the perpendicular distance formula that is the perpendicular distance from point $$\left( {{x}_{1}},{{y}_{1}} \right)$$ to the line $$ax+by+c=0$$ is given as $$\Rightarrow D=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$$ By using the above formula for focus $$\left( 2,3 \right)$$ to the line $$4x-6y+5=0$$ we get $$\begin{aligned} & \Rightarrow \text{Latus rectum}=4\times \left( \dfrac{\left| 4\left( 2 \right)-6\left( 3 \right)+5 \right|}{\sqrt{{{4}^{2}}+{{6}^{2}}}} \right) \\\ & \Rightarrow \text{Latus rectum}=4\left( \dfrac{5}{\sqrt{52}} \right) \\\ \end{aligned}$$ Now, by writing the value of $$\sqrt{52}$$ as $$2\sqrt{13}$$ we get $$\begin{aligned} & \Rightarrow \text{Latus rectum}=4\left( \dfrac{5}{2\sqrt{13}} \right) \\\ & \Rightarrow \text{Latus rectum}=\dfrac{10}{\sqrt{13}} \\\ \end{aligned}$$ Therefore, the length of latus rectum is $$\dfrac{10}{\sqrt{13}}$$ **So, option (b) is the correct answer.** **Note:** This problem can be done in other methods also by using the directrix. The length of the latus rectum is given as $$\Rightarrow \text{Latus rectum}=2\times \left( \text{perpendicular distance from focus to directrix} \right)$$ For finding the directrix we use the result that is the image of focus on the tangent lies on the directrix. For finding the image of point $$\left( h,k \right)$$ on the line $$ax+by+c=0$$ is given as $$\Rightarrow\dfrac{{{x}_{1}}-h}{a}=\dfrac{{{y}_{1}}-k}{b}=\dfrac{-2\left(ah+bk+c\right)}{{{a}^{2}}+{{b}^{2}}}$$. By using the above results we find the equation of the directrix to find the length of the latus rectum.