Question

Two tangents are drawn from a point $( - 2, - 1)$ to the curve ${y^2} = 4x$. If $\alpha$ is the angle between them, then $\left| {\tan \alpha } \right|$ is equal to
A. $\dfrac{1}{3}$
B. $\dfrac{1}{{\sqrt 3 }}$
C. $\sqrt 3$
D. $3$

Answer 1

We draw the tangents to the parabola which have angle $\alpha$ between them. Comparing the general equation of parabola, find the value of a and substitute it in the general equation of tangent to the parabola. Points lying on both the tangents will satisfy the equation of tangent, which will form a quadratic equation in terms of slope of the tangent. From the values of slope of tangents we find the angle between two tangents using the formula.

Formula used:
a) General equation of a parabola is ${y^2} = 4ax$
b) Equation of tangent to a parabola having slope m is $y = mx + \dfrac{a}{m}$.
c) Angle between the two tangents having slope ${m_1},{m_2}$is given by $\left| {\tan \alpha } \right| = \dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}$

Complete step-by-step answer:

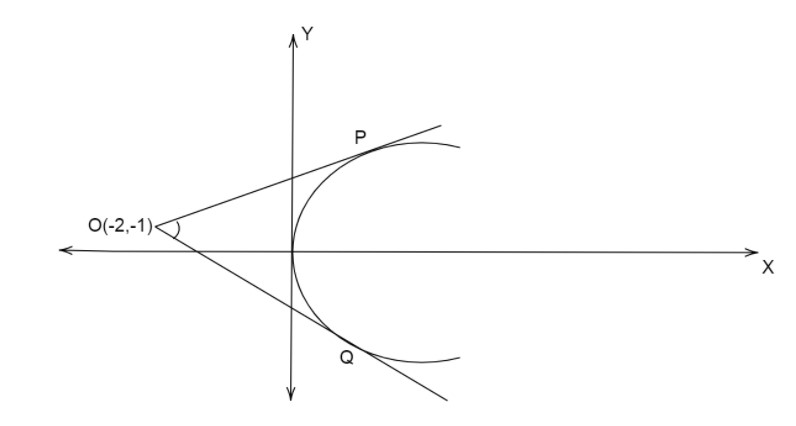
We see that two tangents are drawn to the parabola from point $O( - 2, - 1)$.
We are given the equation of parabola as ${y^2} = 4x$, comparing the general equation of parabola ${y^2} = 4ax$ we get $a = 1$.
Now we know the general equation of tangent to a parabola having slope m is $y = mx + \dfrac{a}{m}$.
Substitute the value of a in the equation of tangent $y = mx + \dfrac{1}{m}$.
Now since the point $O( - 2, - 1)$lies on the tangent, so we put $x = - 2,y = - 1$in the equation

$$\Rightarrow - 1 = m( - 2) + \dfrac{1}{m} \\\ \Rightarrow - 1 = - 2m + \dfrac{1}{m} \\\$$

Take LCM on RHS of the equation
$\Rightarrow - 1 = \dfrac{{ - 2{m^2} + 1}}{m}$
Cross multiply the values
$\Rightarrow - m = - 2{m^2} + 1$
Shift all the values to one side of the equation.
$\Rightarrow 2{m^2} - m - 1 = 0$
Now we factorize the equation by writing $- m = - 2m + m$
$\Rightarrow 2{m^2} - 2m + m - 1 = 0$
Take 2m common from first two terms and 1 common from last two terms
$\Rightarrow 2m(m - 1) + 1(m - 1) = 0$
Collect the factors and write
$\Rightarrow (2m + 1)(m - 1) = 0$
Now we equate each factor to zero
Firstly, $2m + 1 = 0$
$\Rightarrow 2m + 1 = 0$
Shift constant value to one side of the equation.
$\Rightarrow 2m = - 1$
Divide both sides by 2
$\Rightarrow \dfrac{{2m}}{2} = \dfrac{{ - 1}}{2}$
Cancel the common factors from numerator and denominator
$\Rightarrow m = \dfrac{{ - 1}}{2}$
Secondly, $m - 1 = 0$
$\Rightarrow m - 1 = 0$
Shift constant value to one side of the equation.
$\Rightarrow m = 1$
So, we get two slopes ${m_1} = 1,{m_2} = \dfrac{{ - 1}}{2}$
Now we can find the angle between the two tangents using the formula
$\left| {\tan \alpha } \right| = \dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}$.
Substitute ${m_1} = 1,{m_2} = \dfrac{{ - 1}}{2}$
$\Rightarrow \left| {\tan \alpha } \right| = \dfrac{{1 - (\dfrac{{ - 1}}{2})}}{{1 + (\dfrac{{ - 1}}{2} \times 1)}}$
Take LCM in both numerator and denominator

$$\Rightarrow \left| {\tan \alpha } \right| = \dfrac{{\dfrac{{1 + 2}}{2}}}{{\dfrac{{2 - 1}}{2}}} \\\ \Rightarrow \left| {\tan \alpha } \right| = \dfrac{{\dfrac{3}{2}}}{{\dfrac{1}{2}}} \\\$$

Write the fraction in simpler form
$\Rightarrow \left| {\tan \alpha } \right| = \dfrac{3}{2} \times 2$
Cancel the same terms from numerator and denominator.
$\Rightarrow \left| {\tan \alpha } \right| = 3$

So, the correct answer is “Option D”.

Note: Students are likely to make mistake of finding the points P and Q where tangent meets the parabola and then find the equation of line and then find slope and then substitute in formula which is very long calculative process, students can use the direct formula for tangents to the parabola and angle between the tangents.