Question

Two tall buildings are situated $200\,m$ apart. With what speed must a ball be thrown horizontally from the window $540\,m$above the ground in one building, so that it will enter a window $50\,m$ above the ground in the other?

Answer 1

This is an example of horizontal projectile motion. At every point throughout the motion the velocity vector can be represented with its x and y components. Since the acceleration is acting only downwards, the x component of the velocity should not change. In the y direction, we can simply apply the speed equation to get the velocity along the y axis.
The motion equations are
1. $v = u + at$
2. $s = ut + \dfrac{1}{2}a{t^2}$
3. $2as = {v^2} - {u^2}$
Where u is the initial velocity, v is the final velocity, s is the distance covered, t is the time taken and a is the acceleration.
Also, the final velocity is the resultant of the two components. Since the components here are along the x axis and the y axis, the angle between them is ${90^0}$ . And so, the resultant can be calculated as
$v = \sqrt {v_x^2 + v_y^2}$

Complete step by step solution:
Let’s visualize the situation first.

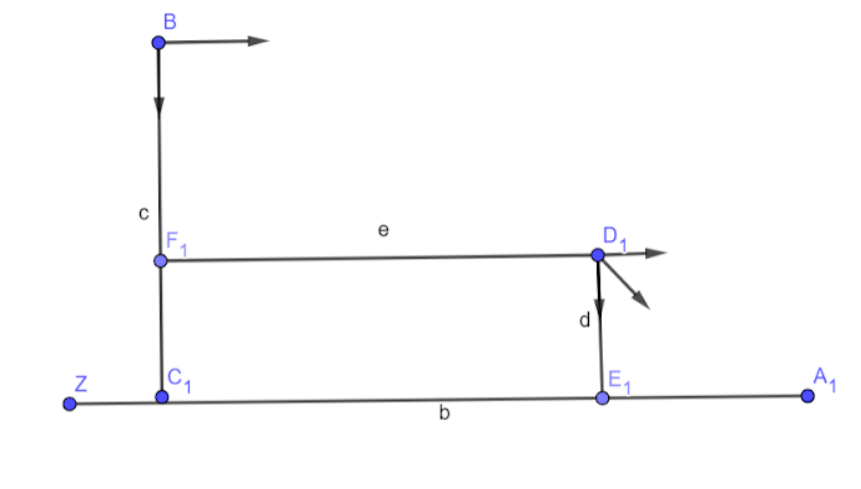
Here $B{C_1}$ represents the $540\,m$ window in one building while ${D_1}{E_1}$ represents the $50\,m$ window in the second building. ${C_1}{E_1}$ represents the distance between the two buildings and is given by ${C_1}{E_1} = 200\,m$.
In y direction,
The distance travelled by ball is given by ${s_y} = 540 - 50 = 490\,m$
The acceleration acting on the ball is given by ${a_y} = + g = 10\,m\,{s^{ - 2}}$
The initial velocity is given as ${u_y} = 0$ (since the ball is projected horizontally it will have a zero-vertical component)
Applying the speed equation $s = ut + \dfrac{1}{2}a{t^2}$ we get,
$\Rightarrow 490 = 0 + \dfrac{1}{2} \times 9.8 \times {t^2}$
$\Rightarrow 100 = {t^2}$
Further solving this,
$t = 10\,s$
In x direction,
The distance travelled by ball is given by ${s_x} = 200\,m$
The acceleration acting on the ball is given by ${a_x} = 0$(since there is no acceleration acting in the x direction)
The initial velocity is given as ${u_x} = u\,m\,{s^{ - 1}}$
Applying the speed equation $s = ut + \dfrac{1}{2}a{t^2}$ we get,
$\Rightarrow 200 = u \times 10 + 0$
$\Rightarrow u = \dfrac{{200}}{{10}}$
$\Rightarrow u = 20\,m\,{s^{ - 1}}$
Hence the ball can be thrown at the $u = 20\,m\,{s^{ - 1}}$.

Note: Always keep a note of the direction of the acceleration. If it is the same as the motion of the object then we take + sign for acceleration. Likewise, if the direction is opposite then we take a – sign. This is also known as retardation. We use the value of g as $10\,m\,{s^{ - 2}}$ to simplify our calculations.