Question

Two tailors P and Q earn Rs. 150 and Rs. 200 per day, respectively. P can stitch 6 shirts and 4 trousers a day, while Q can stitch 10 shirts and 4 trousers per day. How many days should each work to produce at least 60 shirts and 32 trousers at minimum labour cost?

Answer 1

Hint: For solving this LPP (Linear programming problem) we will proceed stepwise first we try to do the formulation of the given data into variables and then determine the objective function and then frame the constraints. Then, try to solve for the answer.

Complete step-by-step answer:
Given:
Two tailors P and Q earn Rs. 150 and Rs. 200 per day, respectively. P can stitch 6 shirts and 4 trousers a day, while Q can stitch 10 shirts and 4 trousers per day.
Formulation:
Now, let tailor P works for $x$ days and tailor Q works for $y$ days.
It is given that cost for tailor P is Rs. 150 and for tailor Q is Rs. 200 per day. Then we have to minimize the combined cost for $x$ days for tailor P and for $y$ days for tailor Q.
Objective function $\left( Z \right)$ :
Total cost in Rs. $=Z=150x+200y$ .
We have to minimise the value of our objective function.
Constraints:
Now, it is given that P can stitch 6 shirts and Q can stitch 10 shirts per day. Then,
Total number of shirts produced by them $=6x+10y$ .
It is given that they have to produce at least 60 shirts. Then, $6x+10y\ge 60$ is our first constraint equation.
Now, it is given that P can stitch 4 trousers and Q can also stitch 4 trousers per day. Then,
Total number of trousers produced was $=4x+4y$ .
It is given that they have to produce at least 32 trousers. Then, $4x+4y\ge 32$ will be another constraint equation. Moreover, two more constraints will be there and they are $x\ge 0$ and $y\ge 0$.

Finally, we have the following constraints:
$\begin{aligned} & 6x+10y\ge 60 \\\ & 4x+4y\ge 32 \\\ & x\ge 0\text{ , y}\ge \text{0} \\\ \end{aligned}$
Now, we will try to plot these constraint equations on a graph. The plot is shown below:

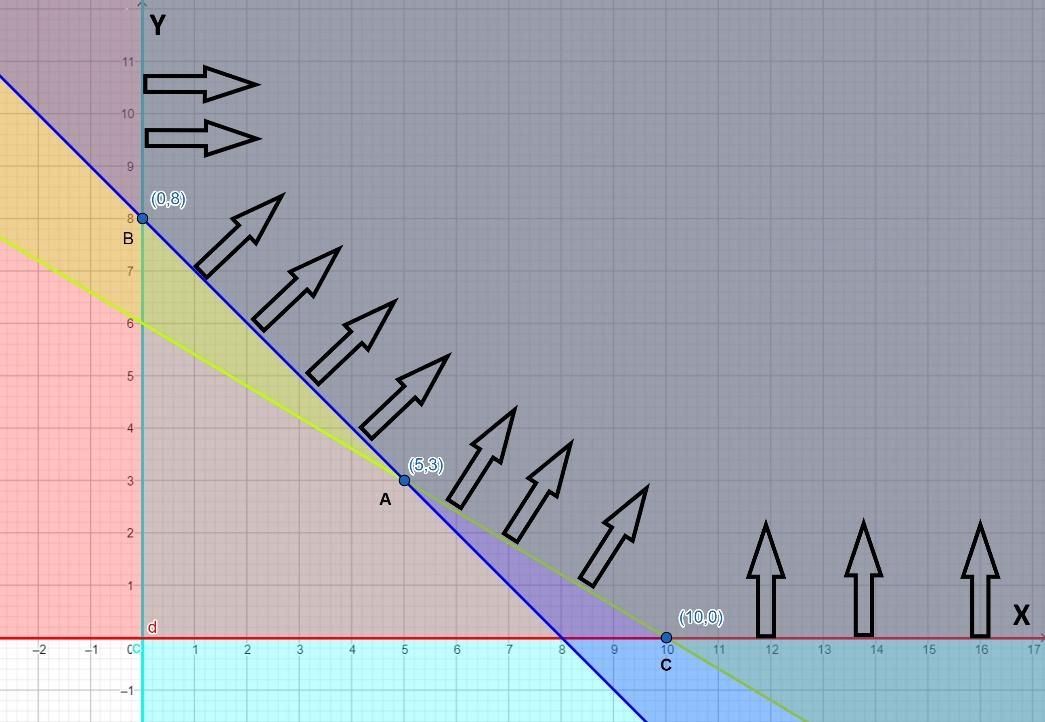
Above graph is plotted as per the constraints written above. From the plot, we conclude that the feasible region is unbounded, and it has three corner points A (5,3) and B (0,8) and C (10,0). Point A is the intersection of $x+y=8$ and $6x+10y=60$ . Point B is the intersection of $x+y=8$ and $y-axis$ . Point C is the intersection of $6x+10y=60$ and $x-axis$ .
Now, we will calculate the value of our objective function at each corner point. It is shown in the table below:

Now, we get the minimum value of our objective function at point A (5,3). But since it is the case of an unbounded region, we have to do the verification for our answer.
Verification:
To verify our result just follow the following steps:
1. Plot $150x+200y\le 1350$ and check whether it has some common region with the feasible region that we got earlier.
2. If there is some common region then, our answer will not be right and if there is no common region then, our answer will be right.
Now, the plot is shown below in which we have plotted $150x+200y\le 1350$ in red colour:

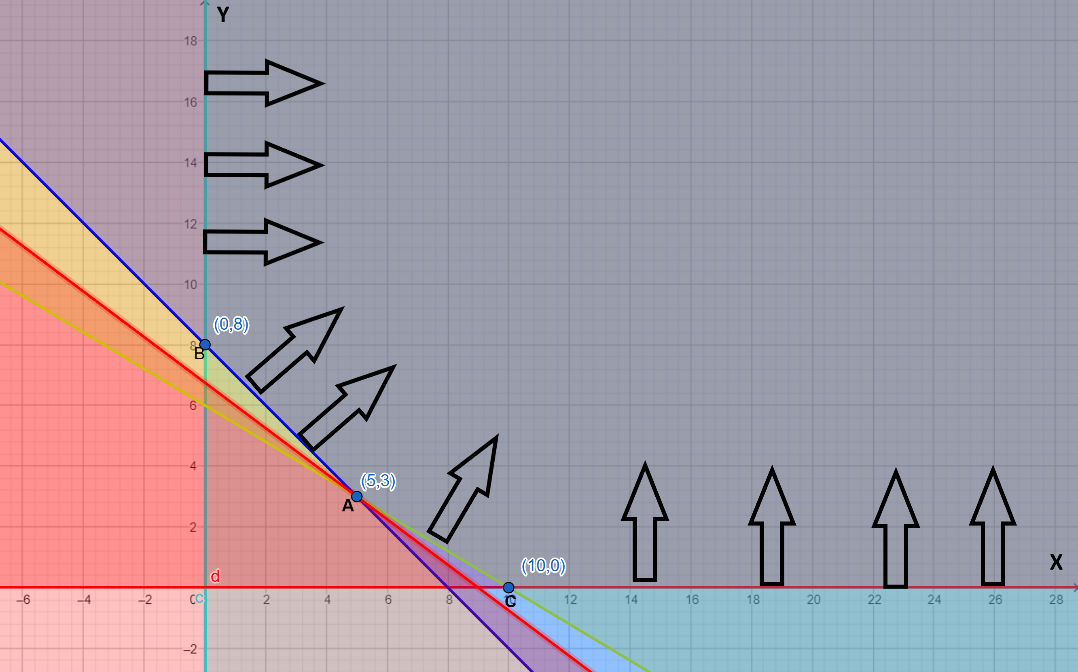
From the above plot, we can say that there is no common region between $150x+200y\le 1350$ and our feasible region. So, our answer is right.
Thus, the minimum value of the objective function will be at point A (5,3).
Hence, to get the desired output in possible cost tailor P should work for 5 days and tailor Q should work for 3 days.

Note: Here, the student should first understand the problem and then proceed stepwise from formulation to the generation of objective function. Then, constraints should be framed accordingly as per the given data. Then, plot the curve carefully and as here the region is unbounded so, don’t forget to verify the result that we got.